题目内容
10．下列4个分式：①$\frac{a+3}{a2+3}$；②$\frac{x-y}{x2-y2}$；③$\frac{m}{2m2n}$；④$\frac{2}{m+1}$，中最简分式有2个．分析 将题目中的式子能化简的先化简，不能化简的式子是最简分式．
解答 解：∵$\frac{a+3}{{a}^{2}+3}=\frac{a+3}{{a}^{2}+3}$，$\frac{x-y}{{x}^{2}-{y}^{2}}=\frac{x-y}{（x+y）（x-y）}=\frac{1}{x+y}$，$\frac{m}{{2m}^{2}n}=\frac{1}{2mn}$，$\frac{2}{m+1}=\frac{2}{m+1}$，
∴最简分式是①④，
故答案为：2．
点评 本题考查最简分式，解题的关键是明确什么是最简分式．
练习册系列答案
春雨教育同步作文系列答案
相关题目
如图，AO⊥CO，BO⊥DO，∠AOD=150°，则∠BOC的度数是30°．
如图，已知菱形ABCD对角线交于点O，AE⊥CD于E，AE=OD，则∠CAE=30°．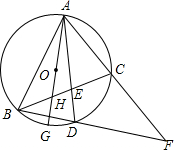
如图，⊙O是△ABC的外接圆，已知AD平分∠BAC交⊙O于点D，连结CD，延长AC，BD，相交于点F．现给出下列结论：