题目内容
15.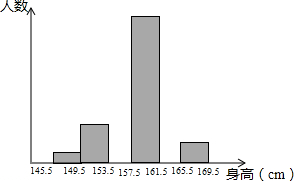 为了解某学校八年级学生的身体发育情况,学校对部分八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图)
为了解某学校八年级学生的身体发育情况,学校对部分八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图)(1)中m和n表示的数分别是多少?
(2)将如表中的数据画成频数分布直方图.
(3)如果全校有2500名女生,则身高在161.5cm以上的约有多少人?
| 组别 | 人数 | 百分比 |
| 145.5~149.5 | 1 | 2% |
| 149.5~153.5 | 4 | 8% |
| 153.5~157.5 | m | 40% |
| 157.5~161.5 | 15 | 30% |
| 161.5~165.5 | 8 | n |
| 165.5~169.5 | 2 | 4% |
| 合计 | 50 | 100% |
分析 (1)由各组的频率之和等于1可得:n=1-其它各组的频率;再由各组的频数之和等于总人数知:m=总人数-其它各组的频数;
(2)根据表格中组距的划分及频数的分布,据此可以绘制频数分布直方图;
(3)根据样本中身高在161.5cm以上的比例乘以总人数可得.
解答 解:(1)m=50-1-4-15-8-2=20,
n=1-0.02-0.08-0.40-0.30-0.04=0.16;
(2)如下图所示:
(3)根据题意,2500×$\frac{8+2}{50}$=500(人),
答:如果全校有2500名女生,则身高在161.5cm以上的约有500人.
点评 本题考查频率及频数的计算,以及动手绘制直方图的能力.记住公式:频率=频数÷总人数是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 如图,在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:
如图,在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:
①∠DBE=∠F;
②2∠BEF=∠BAF+∠C;
③∠F=$\frac{1}{2}$(∠BAC-∠C);
④∠BGH=∠ABE+∠C
其中正确的是( )
 如图,在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:
如图,在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:①∠DBE=∠F;
②2∠BEF=∠BAF+∠C;
③∠F=$\frac{1}{2}$(∠BAC-∠C);
④∠BGH=∠ABE+∠C
其中正确的是( )
| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
10.下列说法正确的是( )
| A. | 25的平方根是5 | B. | -22的算术平方根是2 | ||
| C. | 0.8的立方根是0.2 | D. | $\frac{5}{6}$ 是$\frac{25}{36}$的一个平方根 |
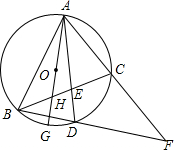 如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,连结CD,延长AC,BD,相交于点F.现给出下列结论:
如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,连结CD,延长AC,BD,相交于点F.现给出下列结论: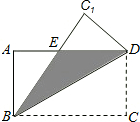 如图,在矩形ABCD中,AB=3,BC=4,如果将该矩形沿对角线BD重叠.
如图,在矩形ABCD中,AB=3,BC=4,如果将该矩形沿对角线BD重叠.