题目内容
12.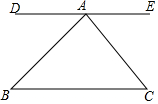 如图,直线DE经过点A,DE∥BC,∠B=45°,∠C=50°,
如图,直线DE经过点A,DE∥BC,∠B=45°,∠C=50°,(1)求∠DAB的度数,并写出理由.
(2)求∠EAC的度数.
(3)计算∠BAC的度数.
(4)根据以上条件及结论,你还能得出其他结论吗?试写出一个.
分析 (1)由平行线的性质可得到∠DAB=∠B;
(2)由平行线的性质可得到∠EAC=∠C;
(3)由平角的定义可求得∠BAC,
(4)结合(1)(2)(3)可得出结论:三角形的内角和是180°.
解答 解:(1)∵DE∥BC,
∴∠DAB=∠B=45°;
(2)∵DE∥BC,
∴∠EAC=∠C=50°,
(3)∵直线DE过点A,
∴∠DAE=180°,
∴∠DAB+∠EAC+∠BAC=180°,
∴∠BAC=180°-45°-50°=95°;
(4)∵DE∥BC,
∴∠B=∠DAB,∠C=∠EAC,
∵∠DAB+∠EAC+∠BAC=180°,
∴∠B+∠C+∠BAC=180°,
即三角形内角和为180°.
点评 本题主要考查平行线的性质,掌握平行线的性质是解题的关键,解题时注意:两直线平行,内错角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图是一个5×5的正方形网格,每个小正方形的边长都是1,请在此网格中画出一个顶点都在格点且面积为17的正方形.
如图是一个5×5的正方形网格,每个小正方形的边长都是1,请在此网格中画出一个顶点都在格点且面积为17的正方形. 如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE折叠压平,使点A与点N重合.
如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE折叠压平,使点A与点N重合.
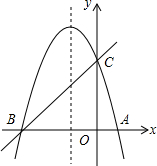 如图,已知抛物线y=-x2+bx+c的对称轴为直线x=-1,与y轴交于点C(0,3),与x轴交于点A和点B.
如图,已知抛物线y=-x2+bx+c的对称轴为直线x=-1,与y轴交于点C(0,3),与x轴交于点A和点B. 如图所示,在长为32m,宽为20m的矩形耕地上,修筑同样宽的三条道路(互相垂直),把耕地分成大小不等的六块试验田,要使试验田的面积为570m2,道路的宽度应为多少?
如图所示,在长为32m,宽为20m的矩形耕地上,修筑同样宽的三条道路(互相垂直),把耕地分成大小不等的六块试验田,要使试验田的面积为570m2,道路的宽度应为多少?