题目内容
7.若$\frac{a}{b+c}$=$\frac{b}{a+c}$=$\frac{c}{a+b}$,则$\frac{a}{b+c}$=-1或$\frac{1}{2}$.分析 分类讨论:当a+b+c=0时,易得$\frac{a}{b+c}$的值;当a+b+c≠0时,根据等比性质易得$\frac{a}{b+c}$的值.
解答 解:当a+b+c=0时,则b+c=-a,所以$\frac{a}{b+c}$=-1;
当a+b+c≠0时,$\frac{a}{b+c}$=$\frac{b}{a+c}$=$\frac{c}{a+b}$=$\frac{a+b+c}{b+c+a+c+a+b}$=$\frac{1}{2}$,
即$\frac{a}{b+c}$的值为-1或$\frac{1}{2}$.
故答案为-1或$\frac{1}{2}$.
故答案为-1或$\frac{1}{2}$.
点评 本题考查了比例的性质:常用的性质有:内项之积等于外项之积;合比性质;分比性质;合分比性质;等比性质.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
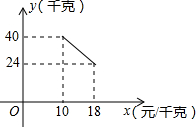 某经销商销售一种产品,这种产品的成本价为10元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克,且10≤x≤18)之间的函数关系如图所示,该经销商想要每天获得150元的销售利润,销售价应定为多少?列出关于x方程是(x-10)(-2x+60)=150(不需化简和解方程).
某经销商销售一种产品,这种产品的成本价为10元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克,且10≤x≤18)之间的函数关系如图所示,该经销商想要每天获得150元的销售利润,销售价应定为多少?列出关于x方程是(x-10)(-2x+60)=150(不需化简和解方程). 如图是由4个大小相同的正方体组合而成的几何体,其俯视图是( )
如图是由4个大小相同的正方体组合而成的几何体,其俯视图是( )



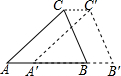 如图,将三角形ABC沿AB方向平移至三角形A1B1C1的位置,连接CC1,AB=5cm,A1B=3cm,∠ABC=35°,CC1=2cm,∠C1CB=35°.
如图,将三角形ABC沿AB方向平移至三角形A1B1C1的位置,连接CC1,AB=5cm,A1B=3cm,∠ABC=35°,CC1=2cm,∠C1CB=35°.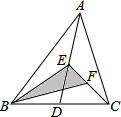 如图,AD是△ABC的中线,点E、F分别为AD、CE的中点,且△ABC的面积是12,则△BEF的面积是3.
如图,AD是△ABC的中线,点E、F分别为AD、CE的中点,且△ABC的面积是12,则△BEF的面积是3. 端午节间,某市一周每天最高气温(单位:℃)情况如图所示,则这组表示最高气温数据的方差=5.35.
端午节间,某市一周每天最高气温(单位:℃)情况如图所示,则这组表示最高气温数据的方差=5.35.