题目内容
12.解方程:(1)4x-3(19-x)=6x-7(9-x)
(2)2-$\frac{1}{2}$(x-1)=$\frac{1}{5}$(x+2)
(3)$\frac{2x+1}{3}$-$\frac{x-1}{6}$=2.
(4)$\frac{3y-1}{4}$-1=$\frac{5y-7}{6}$
(5)$\frac{x+4}{2}$-x+5=$\frac{x+3}{3}$-$\frac{x-2}{6}$.
分析 (1)方程去括号,移项合并,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(3)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(4)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(5)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)去括号得:4x-57+3x=6x-63+7x,
移项合并得:6x=6,
解得:x=1;
(2)去分母得:20-5x+5=2x+4,
移项合并得:7x=21,
解得:x=3;
(3)去分母得:2(2x+1)-(x-1)=12,
去括号得:4x+2-x+1=12,
移项合并得:3x=9,
解得:x=3;
(4)去分母得:3(3y-1)-12=2(5y-7),
去括号得:9y-3-12=10y-14,
移项合并得:y=-1;
(5)去分母得:3x+12-6x+30=2x+6-x+2,
移项合并得:4x=34,
解得:x=8.5.
点评 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.

练习册系列答案
相关题目
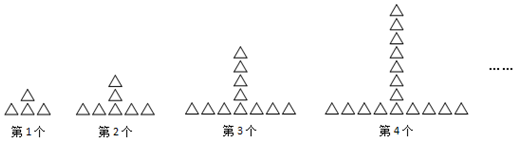
20.如图,每个图形都由同样大小的“△”按照一定的规律组成,其中第1个图形有4个“△”,第2个图形有7个“△”,第3个图形有11个“△”,…,则第8个图形中“△”的个数为( )

| A. | 46 | B. | 48 | C. | 50 | D. | 52 |
4.已知三角形的两边长分别为2和4,第三边的长是方程x2-4x+3=0的解,则这个三角形的周长为( )
| A. | 3 | B. | 9 | C. | 7或9 | D. | 7 |
1.方程2x-(x+10)=5x+2(x+1)的解是( )
| A. | x=$\frac{4}{3}$ | B. | x=-$\frac{4}{3}$ | C. | x=-2 | D. | x=2 |
 在△ABC中,AB=$\sqrt{3}$,BC=4,∠ABC=60°,以AC为斜边作等腰Rt△ACD,连接BD,则BD的长度为$\frac{\sqrt{62}}{2}$.
在△ABC中,AB=$\sqrt{3}$,BC=4,∠ABC=60°,以AC为斜边作等腰Rt△ACD,连接BD,则BD的长度为$\frac{\sqrt{62}}{2}$.
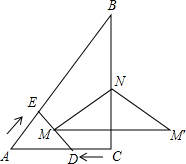 如图,△ABC中,∠C=90°,AC=3,BC=4.点D从C点出发沿射线CA以每秒1个单位长度的速度匀速运动,同时点E从A点出发沿AB以每秒1个单位长度的速度向B点匀速运动,当点E到达B点时D、E都停止运动.点M是DE的中点,直线MN⊥DE交直线BC于点N,点M′与M点关于直线BC对称.点D、E的运动时间为t(秒).
如图,△ABC中,∠C=90°,AC=3,BC=4.点D从C点出发沿射线CA以每秒1个单位长度的速度匀速运动,同时点E从A点出发沿AB以每秒1个单位长度的速度向B点匀速运动,当点E到达B点时D、E都停止运动.点M是DE的中点,直线MN⊥DE交直线BC于点N,点M′与M点关于直线BC对称.点D、E的运动时间为t(秒).