题目内容
20.如图,每个图形都由同样大小的“△”按照一定的规律组成,其中第1个图形有4个“△”,第2个图形有7个“△”,第3个图形有11个“△”,…,则第8个图形中“△”的个数为( )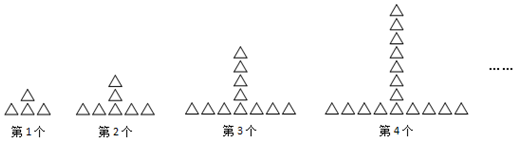
| A. | 46 | B. | 48 | C. | 50 | D. | 52 |
分析 由图形得出第n个图形中“△”个数为2n+1+1+(1+2+3+…+n-1),据此可得.
解答 解:∵第1个图形中“△”个数为3+1+0=4,
第2个图形中“△”个数为5+1+1=7,
第3个图形中“△”个数为7+1+1+2=11,
第4个图形中“△”个数为9+1+1+2+3=16,
∴第8个图形中“△”个数为2×8+1+1+1+2+3+4+5+6+7=46,
故选:A.
点评 本题主要考查图形的变化规律,根据已知图形得出第n个图形中“△”个数为2n+1+1+(1+2+3+…+n-1)是解题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
10.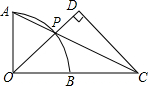 如图,点O为弧AB所在圆的圆心,OA⊥OB,点P在弧AB上,AP的延长线与OB的延长线交于点C,过点C作CD⊥OP于D.若OB=BC=1,则PD的长为( )
如图,点O为弧AB所在圆的圆心,OA⊥OB,点P在弧AB上,AP的延长线与OB的延长线交于点C,过点C作CD⊥OP于D.若OB=BC=1,则PD的长为( )
 如图,点O为弧AB所在圆的圆心,OA⊥OB,点P在弧AB上,AP的延长线与OB的延长线交于点C,过点C作CD⊥OP于D.若OB=BC=1,则PD的长为( )
如图,点O为弧AB所在圆的圆心,OA⊥OB,点P在弧AB上,AP的延长线与OB的延长线交于点C,过点C作CD⊥OP于D.若OB=BC=1,则PD的长为( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
11.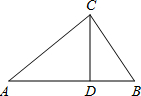 如图,在Rt△ABC中,CD是斜边AB上的高,若BD=4,CD=6,则AD的长为( )
如图,在Rt△ABC中,CD是斜边AB上的高,若BD=4,CD=6,则AD的长为( )
 如图,在Rt△ABC中,CD是斜边AB上的高,若BD=4,CD=6,则AD的长为( )
如图,在Rt△ABC中,CD是斜边AB上的高,若BD=4,CD=6,则AD的长为( )| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
10.某商场将每件进价为20元的玩具以30元的价格出售时,每天可售出300件.经调查当单价每涨1元时,每天少售出10件.若商场想每天获得3750元利润,设每件玩具涨x元,可列方程为:(30+x-20)(300-10x)=3750.对所列方程中出现的代数式,下列说法错误的是( )
| A. | (30+x)表示涨价后玩具的单价 | |
| B. | 10x表示涨价后少售出玩具的数量 | |
| C. | (300-10x)表示涨价后销售玩具的数量 | |
| D. | (30+x-20)表示涨价后的每件玩具的单价 |
 如图,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB=5.
如图,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB=5.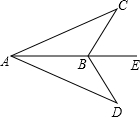 已知:如图,点B在AE上,∠CBA=∠DBA,要使△ABC≌△ABD,还需添加一个条件是BC=BD(填上你认为适当的一个条件即可).
已知:如图,点B在AE上,∠CBA=∠DBA,要使△ABC≌△ABD,还需添加一个条件是BC=BD(填上你认为适当的一个条件即可).