题目内容
18.已知:如图1,在矩形ABCD中,BD是对角线,以BD为斜边向上作等腰直角△EBD,BE交AD于点F,连接AE.(1)若BE=$\sqrt{5}$,AB=$\frac{1}{3}$BC,求矩形ABCD的面积;
(2)若点F是BE中点,求证:AE=$\sqrt{2}$CD;
(3)如图2,若AE=AB,直接写出$\frac{EF}{BD}$的值.

分析 (1)先求出BD,设AB=a,BC=3a,利用勾股定理求出a即可解决问题.
(2)设BF=EF=a,则ED=BE=2a,DF=$\sqrt{5}$a,由△ABF∽△EDF,得到=$\frac{AF}{EF}$=$\frac{AB}{ED}$=$\frac{BF}{DF}$,求出AB、AF,再证明△AFE∽△BFD,求出AE即可解决问题.
(3)如图3中,作EN⊥AD于N,在BC上截取一点M使得BM=DM.先证明△ENF∽△BCD,得$\frac{EF}{BD}$=$\frac{EN}{BC}$,设EN=a,求出BC即可解决问题.
解答 (1)解:如图1中,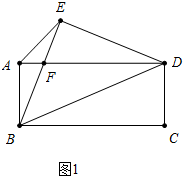
∵BE=ED=$\sqrt{5}$,∠BED=90°,
∴BD=$\sqrt{2}$BE=$\sqrt{10}$,
∵BC=3AB,设AB=a,则BC=3a,
∵四边形ABCD是矩形,
∴∠C=90°,
∴a2+9a2=10,
∴a=1,
∴BC=3,CD=1,
∴矩形ABCD的面积为10.
(2)如图2中,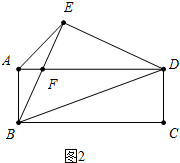
∵BF=EF,设BF=EF=a,则ED=BE=2a,DF=$\sqrt{5}$a,
∵∠AFB=∠EFD,∠BAF=∠FED,
∴△ABF∽△EDF,
∴$\frac{AF}{EF}$=$\frac{AB}{ED}$=$\frac{BF}{DF}$,
∴AF=$\frac{\sqrt{5}}{5}$a,AB=$\frac{2\sqrt{5}}{5}$a,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=2$\sqrt{2}$a,
∵$\frac{AF}{BF}$=$\frac{EF}{DF}$,∠AFE=∠BFD,
∴△AFE∽△BFD,
∴$\frac{AE}{BD}$=$\frac{EF}{DF}$,
∴$\frac{AE}{2\sqrt{2}a}$=$\frac{a}{\sqrt{5}a}$,
∴AE=$\frac{2\sqrt{2}}{\sqrt{5}}$a,
∴$\frac{AE}{CD}$=$\frac{\frac{2\sqrt{2}}{\sqrt{5}}a}{\frac{2\sqrt{5}}{5}a}$=$\sqrt{2}$,
∴AE=$\sqrt{2}$CD.
(3)如图3中,作EN⊥AD于N,在BC上截取一点M使得BM=DM.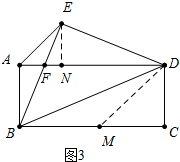
∵AB=AE,
∴∠ABE=∠AEB,
∵△AFE∽△BFD,△ABF∽△EDF,
∴∠AEB=∠BDF,∠ABF=∠EDF,
∴∠EDF=∠ADB=22.5°,
∵∠ENF=∠C=90°,∠EFN=∠BDC=67.5°,
∴△ENF∽△BCD,
∴$\frac{EF}{BD}$=$\frac{EN}{BC}$,设EN=a.
∵∠EAF=∠FBD=45°,
∴∠NAE=∠NEA=45°,
∴AN=EN=a,AE=AB=CD=$\sqrt{2}$a,
∵BM=MD,
∴∠MBD=∠MDB=22.5°,
∴∠DMC=45°=∠MDC,
∴CM=CD=$\sqrt{2}$a,BM=DM=2a,
∴BC=(2+$\sqrt{2}$)a,
∴$\frac{EF}{BD}$=$\frac{EN}{BC}$=$\frac{a}{(2+\sqrt{2})a}$=$\frac{2-\sqrt{2}}{2}$.
点评 本题考查四边形综合题、矩形的性质、等腰直角三角形的性质、相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形,学会添加常用辅助线,属于中考压轴题.

 如图,直线AB∥CD,∠1=55°,∠2=65°,则∠3为( )
如图,直线AB∥CD,∠1=55°,∠2=65°,则∠3为( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
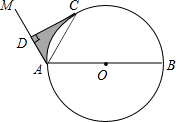 如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D.
如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D. 如图,四边形OABC为直角梯形,已知AB∥OC,BC⊥OC,A点坐标为(3,4),AB=6.
如图,四边形OABC为直角梯形,已知AB∥OC,BC⊥OC,A点坐标为(3,4),AB=6.
 如图,在△ABC中,∠C=90°,∠B=40°,AD是∠BAC的角平分线,求∠ADC的度数.
如图,在△ABC中,∠C=90°,∠B=40°,AD是∠BAC的角平分线,求∠ADC的度数.