题目内容
1.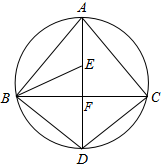 已知,如图,△ABC的三个顶点A,B,C在以AD直径的圆上,且AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
已知,如图,△ABC的三个顶点A,B,C在以AD直径的圆上,且AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.(1)求证:BD=CD;
(2)若∠BCD=∠BAD,请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
分析 (1)利用等弧对等弦即可证明.
(2)利用等弧所对的圆周角相等,∠BAD=∠CBD再等量代换得出∠DBE=∠DEB,从而证明DB=DE=DC,所以B,E,C三点在以D为圆心,以DB为半径的圆上.
解答 证明:(1)∵AB是直径,AD⊥BC,
∴弧BD=弧CD,
∴BD=CD
(2)B,E,C三点在以D为圆心,以DB为半径的圆上.
理由:由(1)知:弧BD=弧CD,
∴∠BAD=∠CBD,
又∵BE平分∠ABC,
∴∠CBE=∠ABE,
∵∠DBE=∠CBD+∠CBE,∠DEB=∠BAD+∠ABE,∠CBE=∠ABE,
∴∠DBE=∠DEB,
∴DB=DE.
由(1)知:BD=CD
∴DB=DE=DC.
∴B,E,C三点在以D为圆心,以DB为半径的圆上.
点评 本题主要考查等弧对等弦,及确定一个圆的条件,此类题是中考的常考题,需要同学们牢固掌握.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
11.无理数a满足:2<a<3,那么a可能是( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{11}$ | D. | $\sqrt{10}$ |
6.下列结论中,错误的有:( )
①所有的菱形都相似;
②放大镜下的图形与原图形不一定相似;
③等边三角形都相似;
④有一个角为110度的两个等腰三角形;
⑤所有的矩形不一定相似.
①所有的菱形都相似;
②放大镜下的图形与原图形不一定相似;
③等边三角形都相似;
④有一个角为110度的两个等腰三角形;
⑤所有的矩形不一定相似.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.下列说法正确的是( )
| A. | -a是单项式,它的系数为1 | |
| B. | $\frac{3}{x}$+3xy-3y2+5是一个多项式 | |
| C. | 多项式x2-2xy+y2是单项式x2、2xy、y2的和 | |
| D. | 如果一个多项式的次数是3,那么这个多项式的任何一项的次数都不大于3 |
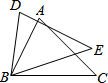 如图,AB=DB,∠ABD=∠CBE,请添加一个适当的条件:BC=BE(只需添加一个即可),使△ABC≌△DBE.理由是SAS.
如图,AB=DB,∠ABD=∠CBE,请添加一个适当的条件:BC=BE(只需添加一个即可),使△ABC≌△DBE.理由是SAS.
 如图,已知BD平分∠ABC,DE⊥AB于E,S=36cm2,AB=18cm,BC=12cm,则DE的长为$\frac{12}{5}$.
如图,已知BD平分∠ABC,DE⊥AB于E,S=36cm2,AB=18cm,BC=12cm,则DE的长为$\frac{12}{5}$.