题目内容
9.已知,在四边形ABCD中,∠ACB+∠ADB=180°,连接AB、CD.△ABC为等边三角形.(1)如图1,求证:∠ADC=∠BDC;
(2)如图2,过点A作AH⊥CD,垂足为H,延长AH交BC于点E,连接BH并延长交AC于F,若AF=CE,请你探究线段CD与AD的数量关系,并证明你的结论.
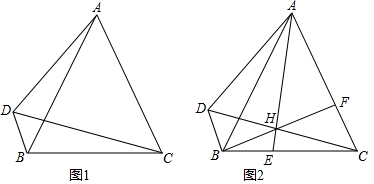
分析 (1)如图1中,作CN⊥DB于N,CM⊥AD于M,只要证明CN=CM,即可解决问题.
(2)如图2中,延长HF到M,使得HA=HM,连接AM.由△ACE≌△BAF,推出∠AHF=60°,推出△AHM是等边三角形,△HCM是Rt△,设DH=a,求出AD,CD即可解决问题.
解答 证明:(1)如图1中,作CN⊥DB于N,CM⊥AD于M,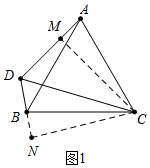
∵△ABC是等边三角形,
∴CA=CB,∠ACB=60°,∵∠ADB+∠ACB=180°,
∴∠ADB=120°,
∵∠N=∠CMD=90°,
∴∠MCN=∠ACB=60°,
∴∠BCN=∠ACM,
在△CNB和△CMA中,
$\left\{\begin{array}{l}{∠N=∠AMC}\\{∠BCN=∠ACM}\\{BC=AC}\end{array}\right.$,
∴△CNB≌△CMA,
∴CN=CM,∵CN⊥DB,CM⊥DA,
∴∠ADC=∠BDC
(2)结论:CD:AD=5:4
理由:如图2中,延长HF到M,使得HA=HM,连接AM.
在△ACE和△BAF中,
$\left\{\begin{array}{l}{AC=AB}\\{∠ACE=∠BAF}\\{CE=AF}\end{array}\right.$,
∴△ACE≌△BAF,
∴∠EAC=∠ABF,
∴∠AHF=∠ABF+∠BAE=∠EAC+∠BAE=60°,
∴△AHM是等边三角形,
易证△AHB≌△AMC,
∴∠ABH=∠ACM,∵∠AFB=∠MFC,
∴∠CMF=∠BAF=60°,
∵AH⊥CD,
∴∠AHD=∠AHC=90°,
∴∠CHM=30°,∠HCM=90°,
设DH=a,则AD=2a,AH=HM=$\sqrt{3}$a,CM=$\frac{\sqrt{3}}{2}$a,CH=$\sqrt{3}$CM=$\frac{3}{2}$a,
∴CD=DH+HC=$\frac{5}{2}$a,
∴CD:AD=$\frac{5}{2}a:2a$=5:4.
点评 此题主要考查了全等三角形的判定和性质、等边三角形的性质.直角三角形30度角性质、勾股定理,角平分线判定定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数解决问题,属于中考常考题型.

 如图,在△ABC和△DEF中,给出以下六个条件中,以其中三个作为已知条件,不能判断△ABC和△DEF全等的是( )
如图,在△ABC和△DEF中,给出以下六个条件中,以其中三个作为已知条件,不能判断△ABC和△DEF全等的是( )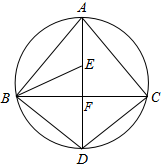 已知,如图,△ABC的三个顶点A,B,C在以AD直径的圆上,且AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
已知,如图,△ABC的三个顶点A,B,C在以AD直径的圆上,且AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.