题目内容
8. 如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题:
如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题:①若AC=AB,则DE=CE;
②若∠C=45°,记△CDE的面积为S1,四边形DABE的面积为S2,则S1=S2,
那么( )
| A. | ①是真命题 ②是假命题 | B. | ①是假命题 ②是真命题 | ||
| C. | ①是假命题 ②是假命题 | D. | ①是真命题 ②是真命题 |
分析 根据等腰三角形的性质得到∠C=∠B,根据圆内接四边形的性质得到∠B=∠CDE,根据等腰三角形的判定判断①;
根据相似三角形的面积比等于相似比的平方判断②.
解答 解:∵AC=AB,
∴∠C=∠B,
∵四边形ABED内接于⊙O,
∴∠B=∠CDE,
∴∠C=∠CDE,
∴DE=CE;①正确;
连接AE,
∵AB是⊙O的直径,
∴∠AEC=90°,又∠C=45°,
∴AC=$\sqrt{2}$CE,
∵四边形ABED内接于⊙O,
∴∠B=∠CDE,∠CAB=∠CED,
∴△CDE∽△CBA,
∴$\frac{{S}_{△CDE}}{{S}_{△CBA}}$=($\frac{CE}{CA}$)2=$\frac{1}{2}$,
∴S1=S2,②正确,
故选:D.
点评 本题考查的是命题的真假判断,掌握圆内接四边形的性质、等腰三角形的性质、相似三角形的判定和性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.若等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形的底边长为( )
| A. | 2cm | B. | 4cm | C. | 6cm | D. | 8cm |
17. 如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4$\sqrt{3}$且∠AFG=60°,GE=2BG,则折痕EF的长为( )
如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4$\sqrt{3}$且∠AFG=60°,GE=2BG,则折痕EF的长为( )
 如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4$\sqrt{3}$且∠AFG=60°,GE=2BG,则折痕EF的长为( )
如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4$\sqrt{3}$且∠AFG=60°,GE=2BG,则折痕EF的长为( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{3}$ |
9.下列运算正确的是( )
| A. | 3a2-2a2=1 | B. | a4•a3=a7 | C. | (a3)2=a5 | D. | (2a)3=6a3 |
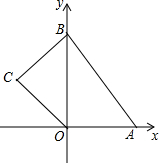 如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A的坐标为(6,0),点B的坐标为(0,8),点C的坐标为(-2$\sqrt{5}$,4),点M,N分别为四边形OABC边上的动点,动点M从点O开始,以每秒1个单位长度的速度沿O→A→B路线向中点B匀速运动,动点N从O点开始,以每秒两个单位长度的速度沿O→C→B→A路线向终点A匀速运动,点M,N同时从O点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间t秒(t>0),△OMN的面积为S.
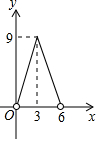
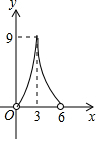
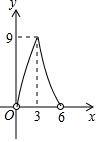
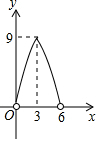
如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A的坐标为(6,0),点B的坐标为(0,8),点C的坐标为(-2$\sqrt{5}$,4),点M,N分别为四边形OABC边上的动点,动点M从点O开始,以每秒1个单位长度的速度沿O→A→B路线向中点B匀速运动,动点N从O点开始,以每秒两个单位长度的速度沿O→C→B→A路线向终点A匀速运动,点M,N同时从O点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间t秒(t>0),△OMN的面积为S.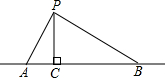 如图,点P在直线AB上方,且∠APB=90°,PC⊥AB于C,若线段AB=6,AC=x,S△PAB=y,则y与x的函数关系图象大致是( )
如图,点P在直线AB上方,且∠APB=90°,PC⊥AB于C,若线段AB=6,AC=x,S△PAB=y,则y与x的函数关系图象大致是( )