题目内容
20.若等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形的底边长为( )| A. | 2cm | B. | 4cm | C. | 6cm | D. | 8cm |
分析 分为两种情况:2cm是等腰三角形的腰或2cm是等腰三角形的底边,然后进一步根据三角形的三边关系进行分析能否构成三角形.
解答 解:若2cm为等腰三角形的腰长,则底边长为10-2-2=6(cm),2+2<6,不符合三角形的三边关系;
若2cm为等腰三角形的底边,则腰长为(10-2)÷2=4(cm),此时三角形的三边长分别为2cm,4cm,4cm,符合三角形的三边关系;
故选A.
点评 此题考查了等腰三角形的两腰相等的性质,同时注意三角形的三边关系:三角形任意两边之和大于第三边.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
8. 如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题:
如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题:
①若AC=AB,则DE=CE;
②若∠C=45°,记△CDE的面积为S1,四边形DABE的面积为S2,则S1=S2,
那么( )
 如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题:
如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题:①若AC=AB,则DE=CE;
②若∠C=45°,记△CDE的面积为S1,四边形DABE的面积为S2,则S1=S2,
那么( )
| A. | ①是真命题 ②是假命题 | B. | ①是假命题 ②是真命题 | ||
| C. | ①是假命题 ②是假命题 | D. | ①是真命题 ②是真命题 |
12. 如图,直线a∥b,∠1=72°,则∠2的度数是( )
如图,直线a∥b,∠1=72°,则∠2的度数是( )
 如图,直线a∥b,∠1=72°,则∠2的度数是( )
如图,直线a∥b,∠1=72°,则∠2的度数是( )| A. | 118° | B. | 108° | C. | 98° | D. | 72° |
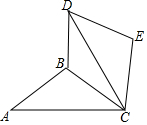 如图,△ABC中,AB=BC=5,AC=8,将△ABC绕点C顺时针方向旋转60°得到△DEC,连接BD,则BD的长度为4$\sqrt{3}$-3.
如图,△ABC中,AB=BC=5,AC=8,将△ABC绕点C顺时针方向旋转60°得到△DEC,连接BD,则BD的长度为4$\sqrt{3}$-3.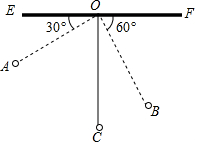 如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求:
如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求: