题目内容
13.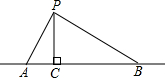 如图,点P在直线AB上方,且∠APB=90°,PC⊥AB于C,若线段AB=6,AC=x,S△PAB=y,则y与x的函数关系图象大致是( )
如图,点P在直线AB上方,且∠APB=90°,PC⊥AB于C,若线段AB=6,AC=x,S△PAB=y,则y与x的函数关系图象大致是( )| A. | 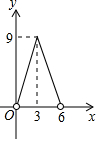 | B. | 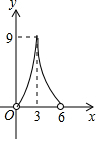 | C. | 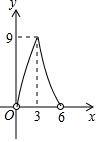 | D. | 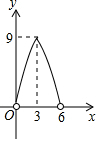 |
分析 根据已知条件推出△APC∽△PBC,根据相似三角形的性质得到PC=$\sqrt{x(6-x)}$,根据三角形的面积公式即可得到结论.
解答 解:∵PC⊥AB于C,∠APB=90°,
∴∠ACP=∠BCP=90°,
∴∠APC+∠BPC=∠APC+∠PAC=90°,
∴∠PAC=∠BPC,
∴△APC∽△PBC,
∴$\frac{PC}{AC}=\frac{BC}{PC}$,
∵AB=6,AC=x,
∴BC=6-x,
∴PC2=x(6-x),
∴PC=$\sqrt{x(6-x)}$,
∴y=$\frac{1}{2}$AB•PC=3$\sqrt{-{x}^{2}+6x}$=3$\sqrt{-(x-3)^{2}+9}$,
故选D.
点评 本题考查了动点问题的函数图象,相似三角形的判定和性质,勾股定理,三角形面积的计算,正确的判定函数的图象是解题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
8. 如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题:
如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题:
①若AC=AB,则DE=CE;
②若∠C=45°,记△CDE的面积为S1,四边形DABE的面积为S2,则S1=S2,
那么( )
 如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题:
如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题:①若AC=AB,则DE=CE;
②若∠C=45°,记△CDE的面积为S1,四边形DABE的面积为S2,则S1=S2,
那么( )
| A. | ①是真命题 ②是假命题 | B. | ①是假命题 ②是真命题 | ||
| C. | ①是假命题 ②是假命题 | D. | ①是真命题 ②是真命题 |
18.一组数据5,7,8,10,12,12,44的众数是( )
| A. | 10 | B. | 12 | C. | 14 | D. | 44 |
2.下列计算正确的是( )
| A. | a2+a3=a5 | B. | a2•a3=a6 | C. | (a2)3=a6 | D. | (ab)2=ab2 |
14.在0.1,3,$\sqrt{2}$和$\frac{1}{3}$这四个实数中,无理数是( )
| A. | 0.1 | B. | 3 | C. | $\sqrt{2}$ | D. | $\frac{1}{3}$ |