题目内容
19.在等腰△ABC中,AD⊥BC交直线BC于点D,若AD=$\frac{1}{2}$BC,则△ABC的顶角的度数为30°或150°或90°.分析 分两种情况;①BC为腰,②BC为底,根据直角三角形30°角所对的直角边等于斜边的一半判断出∠ACD=30°,然后分AD在△ABC内部和外部两种情况求解即可.
解答  解:①BC为腰,
解:①BC为腰,
∵AD⊥BC于点D,AD=$\frac{1}{2}$BC,
∴∠ACD=30°,
如图1,AD在△ABC内部时,顶角∠C=30°,
如图2,AD在△ABC外部时,顶角∠ACB=180°-30°=150°,
②BC为底,如图3,
∵AD⊥BC于点D,AD=$\frac{1}{2}$BC,
∴AD=BD=CD,
∴∠B=∠BAD,∠C=∠CAD,
∴∠BAD+∠CAD=$\frac{1}{2}$×180°=90°,
∴顶角∠BAC=90°,
综上所述,等腰三角形ABC的顶角度数为30°或150°或90°.
故答案为:30°或150°或90°.
点评 本题考查了含30°交点直角三角形的性质,等腰三角形的性质,分类讨论是解题的关键.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
7.$\sqrt{\frac{1}{16}}$的平方根是( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | ±$\frac{1}{4}$ | D. | ±$\frac{1}{2}$ |
14.下表为我省大同市5个空气质量监测站点对某日空气中PM2.5浓度(单位:μg/m3)的检测数据,则这组数据的中位数为( )
| 检测站点 | 果树杨 | 云冈宾馆 | 大同大学 | 安家小村 | 教育学院 |
| PM2.5浓度 | 76μg/m3 | 80μg/m3 | 97μg/m3 | 94μg/m3 | 93μg/m3 |
| A. | 97μg/m3 | B. | 80μg/m3 | C. | 94μg/m3 | D. | 93μg/m3 |
8. 如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题:
如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题:
①若AC=AB,则DE=CE;
②若∠C=45°,记△CDE的面积为S1,四边形DABE的面积为S2,则S1=S2,
那么( )
 如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题:
如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题:①若AC=AB,则DE=CE;
②若∠C=45°,记△CDE的面积为S1,四边形DABE的面积为S2,则S1=S2,
那么( )
| A. | ①是真命题 ②是假命题 | B. | ①是假命题 ②是真命题 | ||
| C. | ①是假命题 ②是假命题 | D. | ①是真命题 ②是真命题 |
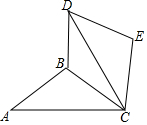 如图,△ABC中,AB=BC=5,AC=8,将△ABC绕点C顺时针方向旋转60°得到△DEC,连接BD,则BD的长度为4$\sqrt{3}$-3.
如图,△ABC中,AB=BC=5,AC=8,将△ABC绕点C顺时针方向旋转60°得到△DEC,连接BD,则BD的长度为4$\sqrt{3}$-3.