题目内容
1．
如图，在△ABC中，∠C=90°，AD是角平分线，AC=12，AD=15，则点D到AB的距离为9．
分析 过点D作DE⊥AB于E，根据角平分线上的点到角的两边距离相等可得DE=CD，再利用勾股定理列式求出CD，即可得解．
解答 
解：如图，过点D作DE⊥AB于E，
∵∠C=90°，AD是角平分线，
∴DE=CD，
由勾股定理得，CD=$\sqrt{A{D}^{2}-A{C}^{2}}$=$\sqrt{1{5}^{2}-1{2}^{2}}$=9，
∴DE=9，
即点D到AB的距离为9．
故答案为：9．
点评 本题考查了角平分线上的点到角的两边距离相等的性质，勾股定理的应用，熟记性质是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
12．用代数式表示“a的平方的2倍与b的商”正确的是（ ）
| A． | 2a2÷b | B． | （2a）÷b | C． | $\frac{2{a}^{2}}{b}$ | D． | $\frac{b}{2{a}^{2}}$ |
6．等腰三角形的两条边长分别为3cm和6cm，则它的周长为（ ）
| A． | 12cm | B． | 15cm | C． | 12或15cm | D． | 18cm或36cm |
13．
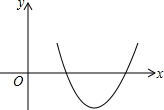二次函数y=ax2+bx+c的图象如图所示，判断方程ax2+bx+c=0的两根，下列叙述正确的是（ ）
二次函数y=ax2+bx+c的图象如图所示，判断方程ax2+bx+c=0的两根，下列叙述正确的是（ ）| A． | 有两个不相等的正根 | B． | 有两个相等的正根 | ||
| C． | 有一正一负两个根 | D． | 没有实数根 |
11．
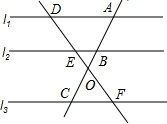如图l1∥l2∥l3，直线AC与DF交于点O，且与l1，l2，l3分别交于点A，B，C，D，E，F，则下列比例式不正确的是（ ）
如图l1∥l2∥l3，直线AC与DF交于点O，且与l1，l2，l3分别交于点A，B，C，D，E，F，则下列比例式不正确的是（ ）| A． | $\frac{AB}{BC}$=$\frac{DE}{EF}$ | B． | $\frac{AB}{BO}$=$\frac{DE}{EO}$ | C． | $\frac{OB}{OC}$=$\frac{OE}{OF}$ | D． | $\frac{AD}{CF}$=$\frac{AO}{AC}$ |