题目内容
14．已知一元二次方程有一个根是2，另一个根是-4，那么这个方程可以是x2+2x-4=0（填一个正确的方程即可）．分析 先计算2与-4的和与积，然后根据根与系数的关系写出满足题意的方程．
解答 解：∵2+（-4）=-2，2×（-4）=-8，
∴以2和-4为根的方程可为x2+2x-4=0．
故答案为x2+2x-4=0．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
相关题目
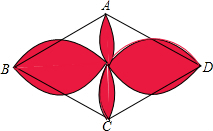如图，四边形ABCD是菱形，AB=10cm，∠ABC=60°，分别以ABCD的四条边为直径作半圆．求图中红色部分的面积．
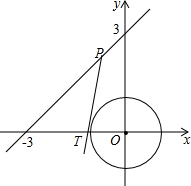如图，在直角坐标系中，圆O是以坐标原点为圆心，半径为1的圆，直线L的方程为x-y+3=0，在L上任取一点P作圆O的切线，切点为T，则PT长的最小值是$\frac{\sqrt{14}}{2}$．
3．若a＜b＜0，化简$\root{3}{{{{（{a-b}）}^3}}}-\sqrt{{{（{a-b}）}^2}}+\root{3}{a^3}-\sqrt{b^2}$的结果为（ ）
| A． | 3a-b | B． | 3（b-a） | C． | a-b | D． | b-a |
4．下列二次根式是最简二次根式的是（ ）
| A． | $\sqrt{2a}$ | B． | $\sqrt{\frac{b}{3}}$ | C． | $\sqrt{{c}^{3}}$ | D． | $\sqrt{8{d}^{2}}$ |