题目内容
3.已知$\frac{a}{b}$=$\frac{c}{d}$=$\frac{1}{2}$,则下列式子中正确的是( )| A. | $\frac{a}{b}$=$\frac{{c}^{2}}{{d}^{2}}$ | B. | $\frac{a}{d}$=$\frac{c}{b}$ | C. | $\frac{a+c+1}{b+d+2}$=$\frac{1}{2}$ | D. | $\frac{a+c}{b+d+2}$=$\frac{1}{2}$ |
分析 利用等式的性质对A进行判断;直接由已知条件对B进行判断;根据等比性质对C、D进行判断.
解答 解:A、因为$\frac{a}{b}$=$\frac{c}{d}$=$\frac{1}{2}$,则$\frac{{c}^{2}}{{d}^{2}}$=$\frac{1}{4}$,所以A选项错误;
B、$\frac{a}{b}$=$\frac{c}{d}$=$\frac{1}{2}$,所以B选项错误;
C、因为$\frac{a}{b}$=$\frac{c}{d}$=$\frac{1}{2}$,则$\frac{a+c+1}{b+d+2}$=$\frac{1}{2}$,所以C选项正确;
D、因为$\frac{a}{b}$=$\frac{c}{d}$=$\frac{1}{2}$,则$\frac{a+c+1}{b+d+2}$=$\frac{1}{2}$,所以D选项错误.
故选C.
点评 本题考查了比例的性质:常用的性质有:内项之积等于外项之积;合比性质;分比性质;合分比性质;等比性质.

练习册系列答案
相关题目
 如图,△ABC≌△BAD,A与B,C与D是对应点,若AB=4cm,BD=4.5cm,AD=1.5cm,则BC=1.5cm.
如图,△ABC≌△BAD,A与B,C与D是对应点,若AB=4cm,BD=4.5cm,AD=1.5cm,则BC=1.5cm.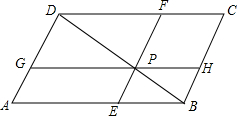 如图,在?ABCD中,P是对角线BD上的任意一点,过点P作EF∥BC,分别与AB,CD相交于点E,F;过点P再作GH∥AB,分别与AD,BC相交于点G,H,图中有几个平行四边形?其中哪几对平行四边形面积相等?为什么?
如图,在?ABCD中,P是对角线BD上的任意一点,过点P作EF∥BC,分别与AB,CD相交于点E,F;过点P再作GH∥AB,分别与AD,BC相交于点G,H,图中有几个平行四边形?其中哪几对平行四边形面积相等?为什么?