题目内容
13．
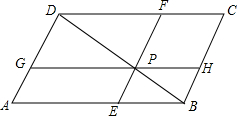如图，在?ABCD中，P是对角线BD上的任意一点，过点P作EF∥BC，分别与AB，CD相交于点E，F；过点P再作GH∥AB，分别与AD，BC相交于点G，H，图中有几个平行四边形？其中哪几对平行四边形面积相等？为什么？
分析 由平行四边形的判定方法容易得出图中的平行四边形有9个；由平行四边形的一条对角线可以把平行四边形分成两个全等的三角形，面积相等，得出S?AEPG=S?HCFP，得出S?ABHG=S?BCFE，S?AEFD=S?HCDG．
解答 解：图中有9个平行四边形；其中有3对对平行四边形面积相等S?ABHG=S?BCFE，S?AGPE=S?HCFP，S?AEFD=S?HCDG．
理由如下：
∵四边形ABCD是平行四边形，
∴AB∥CD，AD∥BC，
∵EF∥BC，GH∥AB，
∴AD∥EF∥BC，AB∥GH∥CD，
∴图中的平行四边形有：?ABCD，?ABHG，?GHCD，?AEFD，?BCFE，?AEPG，?BHPE，?PFDG，?PHCF共9个．
∵四边形ABCD是平行四边形，
∴S△ABD=S△CBD．
∵BP是平行四边形BEPH的对角线，
∴S△BEP=S△BHP，
∵PD是平行四边形GPFD的对角线，
∴S△GPD=S△FPD．
∴S△GPD=S△FPD．
∴S△ABD-S△BEP-S△GPD=S△BCD-S△BHP-S△PFD，
即S?AEPG=S?HCFP，
∴S?ABHG=S?BCFE，
同理S?AEFD=S?HCDG．
即：S?ABHG=S?BCFE，S?AGPE=S?HCFP，S?AEFD=S?HCDG．
点评 此题考查了平行四边形的判定与性质、三角形的面积；熟练掌握平行四边形的判定方法，熟记平行四边形的一条对角线可以把平行四边形分成两个全等的三角形是解决问题的关键．
练习册系列答案
名校课堂系列答案
相关题目
3．已知$\frac{a}{b}$=$\frac{c}{d}$=$\frac{1}{2}$，则下列式子中正确的是（ ）
| A． | $\frac{a}{b}$=$\frac{{c}^{2}}{{d}^{2}}$ | B． | $\frac{a}{d}$=$\frac{c}{b}$ | C． | $\frac{a+c+1}{b+d+2}$=$\frac{1}{2}$ | D． | $\frac{a+c}{b+d+2}$=$\frac{1}{2}$ |
已知一个礼品盒的长、宽、高分别是12cm，8cm，2cm．现有4盒礼品，用下列两种方式包装．请问：哪种方式更省包装纸？
5．下列判断正确的是（ ）
| A． | 方程是等式，等式就是方程 | B． | 方程是含有未知数的等式 | ||
| C． | 方程的解就是方程的根 | D． | 方程2x=3x没解 |
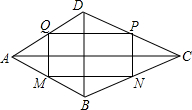已知：如图，在四边形ABCD中，AB=AD，CB=CD，点M，N，N，P，Q分别是AB，BC，CD，DA的中点，求证：四边形MNPQ是矩形．
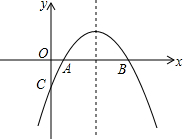如图抛物线y=-x2+bx+c与x轴的两个交点别为A（1，0），B（3，0）