题目内容
13.某品牌饮水机生产一种饮水机和饮水机槽,饮水机每台定价350元,饮水机桶每只定价50元,长方开展促销活动期间,可以同时向客户提供两种优惠方案:(1)买一台饮水机送一只饮水机桶;(2)饮水机和饮水机桶都按定价的90%付款,现某客户到该饮水机厂购买饮水机30台,饮水机桶x只(x超过30).(1)若该客户按方案(1)购买,求客户需付款(用含x的式子表示);
(2)若该客户按方案(2)购买,求客户需付款(用含x的式子表示);
(3)当x=40时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.
分析 (1)(2)按照对应的方案的计算方法分别列出代数式即可;
(3)把x=40代入求得的代数式求得数值,进一步比较得出答案即可.
解答 解:(1)客户按方案(1)购买需付款30×350+(x-30)×50=50x+30(350-50)=(50x+9000)元;
(2)客户按方案(2)购买需付款350×90%×30+50×90%×x=(45x+9450)元;
(3)当x=40时,
方案一需50×40+9000=11000元;
方案二需45×40+9450=11250元;
所以按方案一购买合算;
先按方案一购买30台饮水机,送30只饮水机桶需10500元,差10只饮水机桶按方案二购买需450元,共需10950元.
点评 此题考查列代数式,理解两种方案的优惠方案,得出运算的方法是解决问题的关键.

练习册系列答案
相关题目
3.在Rt△ABC中,斜边AB=3,则AB2+AC2+BC2=( )
| A. | 9 | B. | 18 | C. | 10 | D. | 24 |
4.一元二次方程x2-2x-1=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
3.已知$\frac{a}{b}$=$\frac{c}{d}$=$\frac{1}{2}$,则下列式子中正确的是( )
| A. | $\frac{a}{b}$=$\frac{{c}^{2}}{{d}^{2}}$ | B. | $\frac{a}{d}$=$\frac{c}{b}$ | C. | $\frac{a+c+1}{b+d+2}$=$\frac{1}{2}$ | D. | $\frac{a+c}{b+d+2}$=$\frac{1}{2}$ |
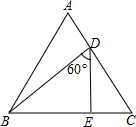 如图,△ABC为正三角形,D、E分别是AC、BC上的动点,当∠BDE=60°时,
如图,△ABC为正三角形,D、E分别是AC、BC上的动点,当∠BDE=60°时,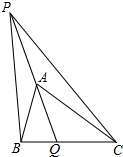 如图,在△ABC中,AQ是△ABC的角平分线,P是QA延长线上一点.若∠BPC=$\frac{1}{2}$∠BAC,PB:PC=1:2,BQ=1,则CQ的长为4.
如图,在△ABC中,AQ是△ABC的角平分线,P是QA延长线上一点.若∠BPC=$\frac{1}{2}$∠BAC,PB:PC=1:2,BQ=1,则CQ的长为4.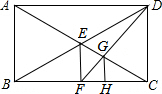 已知:如图,在矩形ABCD中,AC,BD交于点E.
已知:如图,在矩形ABCD中,AC,BD交于点E.