题目内容
9．
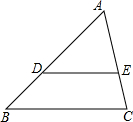如图，在△ABC中，D、E分别是边AB、AC上的点，且DE∥BC，若△ADE与△ABC的周长之比为2：3，AD=4，则DB=2．
分析 由DE∥BC，易证△ADE∽△ABC，由相似三角形的性质即可求出AB的长，进而可求出DB的长．
解答 解：∵DE∥BC，
∴△ADE∽△ABC，
∵△ADE与△ABC的周长之比为2：3，
∴AD：AB=2：3，
∵AD=4，
∴AB=6，
∴DB=AB-AD=2，
故答案为：2．
点评 此题主要考查的是相似三角形的性质：相似三角形的一切对应线段（包括对应边、对应中线、对应高、对应角平分线等）的比等于相似比，面积比等于相似比的平方．
练习册系列答案
相关题目
20．
如图，点A、B、C都在⊙O上，若∠ACB=29°，则∠AOB的度数为（ ）
如图，点A、B、C都在⊙O上，若∠ACB=29°，则∠AOB的度数为（ ）| A． | 14.5° | B． | 29° | C． | 58° | D． | 61° |
如图，在半径为3的⊙O中，直径AB与弦CD相交于点E，连接AC，BD，若AC=2，则tanD=2$\sqrt{2}$．
如图，OA=2，以点A为圆心，1为半径画⊙A与OA的延长线交于点C，过点A画OA的垂线，垂线与⊙A的一个交点为B，连接BC
解不等式2x-1＞$\frac{3x-1}{2}$，并把它的解集在数轴上表示出来．
19．
三本相同的书本叠成如图所示的几何体，它的主视图是（ ）
三本相同的书本叠成如图所示的几何体，它的主视图是（ ）| A． |  | B． |  | C． |  | D． |  |