题目内容
19.已知二次函数y=x2+bx+c与x轴只有一个交点,且图象过A(x1,m)、B(x1+n,m)两点,则m、n的关系为( )| A. | m=$\frac{1}{2}$n | B. | m=$\frac{1}{4}$n | C. | m=$\frac{1}{2}$n2 | D. | m=$\frac{1}{4}$n2 |
分析 由“抛物线y=x2+bx+c与x轴只有一个交点”推知x=-$\frac{b}{2}$时,y=0.且b2-4c=0,即b2=4c,其次,根据抛物线对称轴的定义知点A、B关于对称轴对称,故A(-$\frac{b}{2}$-$\frac{n}{2}$,m),B(-$\frac{b}{2}$+$\frac{n}{2}$,m);最后,根据二次函数图象上点的坐标特征即可得出结论.
解答 解:∵抛物线y=x2+bx+c与x轴只有一个交点,
∴当x=-$\frac{b}{2}$时,y=0.且b2-4c=0,即b2=4c.
又∵点A(x1,m),B(x1+n,m),
∴点A、B关于直线x=-$\frac{b}{2}$对称,
∴A(-$\frac{b}{2}$-$\frac{n}{2}$,m),B(-$\frac{b}{2}$+$\frac{n}{2}$,m),
将A点坐标代入抛物线解析式,得m=(-$\frac{b}{2}$-$\frac{n}{2}$)2+(-$\frac{b}{2}$-$\frac{n}{2}$)b+c,即m=$\frac{{n}^{2}}{4}$-$\frac{{b}^{2}}{4}$+c,
∵b2=4c,
∴m=$\frac{1}{4}$n2,
故选D.
点评 本题考查的是抛物线与x轴的交点问题,根据题意得出抛物线的对称轴方程是解答此题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
5.为了方便市民出行,提倡低碳交通,近几年南京市大力发展公共自行车系统,根据规划,全市公共自行车总量明年将达70000辆,用科学记数法表示70000是( )
| A. | 0.7×105 | B. | 7×104 | C. | 7×105 | D. | 70×103 |
10.已知甲、乙、丙均为x的一次多项式,且其一次项的系数皆为正整数.若甲与乙相乘为x2-4,乙与丙相乘为x2+15x-34,则甲与丙相加的结果与下列哪一个式子相同?( )
| A. | 2x+19 | B. | 2x-19 | C. | 2x+15 | D. | 2x-15 |
4.下列四个数中最大的数是( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
8.在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8、7、9、8、8
乙:7、9、6、9、9
则下列说法中错误的是( )
甲:8、7、9、8、8
乙:7、9、6、9、9
则下列说法中错误的是( )
| A. | 甲、乙得分的平均数都是8 | |
| B. | 甲得分的众数是8,乙得分的众数是9 | |
| C. | 甲得分的中位数是9,乙得分的中位数是6 | |
| D. | 甲得分的方差比乙得分的方差小 |

 如图,OA=2,以点A为圆心,1为半径画⊙A与OA的延长线交于点C,过点A画OA的垂线,垂线与⊙A的一个交点为B,连接BC
如图,OA=2,以点A为圆心,1为半径画⊙A与OA的延长线交于点C,过点A画OA的垂线,垂线与⊙A的一个交点为B,连接BC (1)解方程组:$\left\{\begin{array}{l}{x-y=2}\\{x-y=y+1}\end{array}\right.$.
(1)解方程组:$\left\{\begin{array}{l}{x-y=2}\\{x-y=y+1}\end{array}\right.$.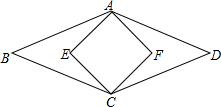 如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为13cm.
如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为13cm.