题目内容
2.已知抛物线y=a(x-1)2+k经过点(2,-7),(3,-13).(1)求a,k的值;
(2)写出该抛物线的开口方向及顶点坐标;
(3)当x取何值时,y随x的增大而增大?
分析 (1)把已知点的坐标代入可求得a、k的值;
(2)由抛物线的顶点式可求得其开口方向及顶点坐标;
(3)可先求得抛物线的对称轴,再利用二次函数的增减性可求得答案.
解答 解:
(1)∵抛物线y=a(x-1)2+k经过点(2,-7),(3,-13),
∴$\left\{\begin{array}{l}{a(2-1)^{2}+k=-7}\\{a(3-1)^{2}+k=-13}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-2}\\{k=-5}\end{array}\right.$;
(2)由(1)可知抛物线的解析式为y=-2(x-1)2-5,
∵-2<0,
∴抛物线开口向下,顶点坐标为(1,-5);
(3)由(2)可知抛物线对称轴为x=1,且开口向下,
∴当x<1时,y随x的增大而增大.
点评 本题主要考查二次函数的性质,掌握函数图象上的点的坐标满足函数解析式是解题关键.

练习册系列答案
相关题目
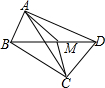 如图,在四边形ABCD中,∠BAD=∠BCD=90°,M是BD的中点,连接AM、CM,那么△MAC是等腰三角形吗?请说明理由.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,M是BD的中点,连接AM、CM,那么△MAC是等腰三角形吗?请说明理由.