题目内容
13．
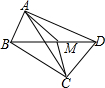如图，在四边形ABCD中，∠BAD=∠BCD=90°，M是BD的中点，连接AM、CM，那么△MAC是等腰三角形吗？请说明理由．
分析 先根据O是BD的中点可知，OA．OC分别是Rt△ABD与Rt△BCD的中线，可知OA=OC，再根据等边对等角即可求出∠OAC=∠OCA．
解答 解：△MAC是等腰三角形，
理由：∵△ABD是直角三角形，M为BD的中点，
∴MA=$\frac{1}{2}$BD（直角三角形斜边中线等于斜边一半），
∵△BDC是直角三角形，M为BD的中点，
∴MC=$\frac{1}{2}$BD，
∴MA=MC，
∴∠MAC=∠MCA，
∴△MAC是等腰三角形．
点评 本题考查的是等腰三角形的判定和性质，直角三角形的性质，即直角三角形斜边的中线等于斜边的一半．
练习册系列答案
相关题目
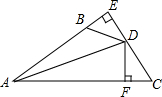如图，DE⊥AB于E，DF⊥AC于F，若BD=CD，BE=CF，则下列结论：
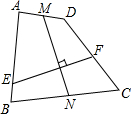如图，四边形ABCD中，AB=CD，M，N分别为AD，BC的中点，EF⊥MN交AB于点E，交CD于点F．求证：∠AEF=∠DFE．
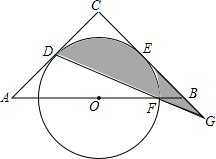如图，已知△ABC，AC=BC=6，∠C=90°，O是AB的中点，⊙O与AC相切于点D，与BC相切于点E．⊙O交OB于F，连接DF并延长交CB的延长线于G．