题目内容
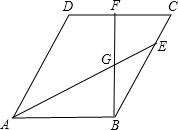 如图,平行四边形ABCD中,AE平分∠DAB,BF⊥DC交AE于点G,且BF=AB
如图,平行四边形ABCD中,AE平分∠DAB,BF⊥DC交AE于点G,且BF=AB(1)若∠C=60°,BE=
| 3 |
(2)证明:AD=BG+FC.
考点:平行四边形的性质,全等三角形的判定与性质
专题:
分析:(1)利用等角对等边即可证明BA=BE,在直角△ABG中求的BG和AB的长,根据FG=BF-BG即可求解;
(2)作CH⊥AB于点H,延长AH到I,使HI=BG,则BI=BG+FC,然后证明△BCI是等腰三角形即可.
(2)作CH⊥AB于点H,延长AH到I,使HI=BG,则BI=BG+FC,然后证明△BCI是等腰三角形即可.
解答:解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,∠C=∠BAD=60°,CD∥AB,
∴∠1=∠3,
∵AE平分∠DAB,
∴∠1=∠2=30°,
∴∠2=∠3,
∴AB=BE=
,
∵BF⊥DC,
∴∠DFB=90°,
∵CD∥AB,
∴∠ABF=90°,
∴BG=
AG,
在Rt△ABG中:AG2=AB2+BG2,
∴(2BG)2=(
)2+BG2,
解得:BG=1,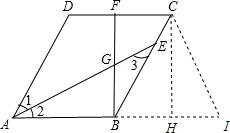
又∵BF=AB,
∴FG=BF-BG=
-1;
(2)作CH⊥AB于点H,延长AH到I,使HI=BG.
则四边形BFCH是矩形,
则CF=BH,CH=BF=AB.
在△ABG和△CHI中,
,
∴△ABG≌△CHI(SAS).
∴∠I=∠AGB,∠ICH=∠2,
∴∠ICH=∠3,
∵BF∥CH,
∴∠FBE=∠BCH,
又∵∠I=∠AGB=∠3+∠ABE,∠BCI=∠BCH+∠ICH,
∴∠BCI=∠I,
∴BC=BI=BH+HI.
又∵BH=FC,HI=BG,平行四边形ABCD中AD=BC,
∴AD=BG+FC.
∴AD∥BC,∠C=∠BAD=60°,CD∥AB,
∴∠1=∠3,
∵AE平分∠DAB,
∴∠1=∠2=30°,
∴∠2=∠3,
∴AB=BE=
| 3 |
∵BF⊥DC,
∴∠DFB=90°,
∵CD∥AB,
∴∠ABF=90°,
∴BG=
| 1 |
| 2 |
在Rt△ABG中:AG2=AB2+BG2,
∴(2BG)2=(
| 3 |
解得:BG=1,

又∵BF=AB,
∴FG=BF-BG=
| 3 |
(2)作CH⊥AB于点H,延长AH到I,使HI=BG.
则四边形BFCH是矩形,
则CF=BH,CH=BF=AB.
在△ABG和△CHI中,
|
∴△ABG≌△CHI(SAS).
∴∠I=∠AGB,∠ICH=∠2,
∴∠ICH=∠3,
∵BF∥CH,
∴∠FBE=∠BCH,
又∵∠I=∠AGB=∠3+∠ABE,∠BCI=∠BCH+∠ICH,
∴∠BCI=∠I,
∴BC=BI=BH+HI.
又∵BH=FC,HI=BG,平行四边形ABCD中AD=BC,
∴AD=BG+FC.
点评:本题考查了平行四边形的性质,等腰三角形的判定定理以及全等三角形的判定与性质,作出辅助线是关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 已知,如图,∠C=90°,∠A=30°,BD⊥AD于D,DC∥AB,AB=10,求CD的长.
已知,如图,∠C=90°,∠A=30°,BD⊥AD于D,DC∥AB,AB=10,求CD的长.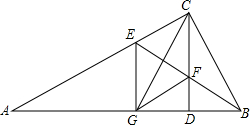 Rt△ABC中,CD是斜边AB上的高,BE平分∠CBA交AC于E,交CD于F,CG⊥BE交AB于G.
Rt△ABC中,CD是斜边AB上的高,BE平分∠CBA交AC于E,交CD于F,CG⊥BE交AB于G. 如图,在矩形ABCD中,E、F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
如图,在矩形ABCD中,E、F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
 如图,在△ABC中,D为BC边的中点,点E在线段AD上,BE的延长线交AC边于点F,若AE:ED=1:3,AF=2,求线段FC的长.
如图,在△ABC中,D为BC边的中点,点E在线段AD上,BE的延长线交AC边于点F,若AE:ED=1:3,AF=2,求线段FC的长. 已知如图,四边形ABCD的边长是2的菱形,且∠CDA=30°,CF⊥x轴,求点D关于CF的对称点D′的坐标.
已知如图,四边形ABCD的边长是2的菱形,且∠CDA=30°,CF⊥x轴,求点D关于CF的对称点D′的坐标. 如图,矩形ABCO,点E在AB上,且BE=2AE,点F在BC上,双曲线y=
如图,矩形ABCO,点E在AB上,且BE=2AE,点F在BC上,双曲线y=