题目内容
17. 如图,在△ABC中,AB=AC,∠A=36°,两条角平分线BD、CE相交于点O,则图中全等等腰三角形有3对.
如图,在△ABC中,AB=AC,∠A=36°,两条角平分线BD、CE相交于点O,则图中全等等腰三角形有3对.
分析 由在△ABC中,AB=AC,∠A=36°,角平分线BD与CE相交于点O,利用等边对等角与角平分线的性质,易求得图中各角的度数,然后利用等角对等边的知识,即可判定△ABC,△ABE,△ACD,△BCD,△BCE,△OBC,△OBD,△OCE都是等腰三角形.
解答 解:∵在△ABC中,AB=AC,∠A=36°,
∴∠ABC=∠ACB=$\frac{1}{2}$(180°-∠A)=72°,
∵△ABC的角平分线BE与CD相交于点O,
∴∠ABE=∠EBC=$\frac{1}{2}$∠ABC=36°,∠ACD=∠BCD=$\frac{1}{2}$∠ACB=36°,
∴∠BDC=∠BEC=180°-36°-72°=72°,
∴∠A=∠ABE=∠EBC=∠BCD=∠ACD=36°,∠ABC=∠ACB=∠BEC=∠BDC=72°,
∴∠DOB=∠EOC=180°-72°-36°=72°,
∴AE=BE,AD=CD,BD=OB=OC=CE,CD=BC=BE,
∴等腰三角形有:△ABC,△ABE,△ACD,△BCD,△BCE,△OBC,△OBD,△OCE共8个,其中△ABE≌△ACD,
△BCD≌△BCE,△OBD≌△OCE.
故答案为:3对.
点评 此题考查了等腰三角形的性质与判定以及角平分线的定义.此题难度适中,注意数形结合思想的应用,小心别漏解.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
5.已知△ABC≌△DEF,∠A=70°,∠E=50°,则∠F的度数为( )
| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
12.下列说法不正确的是( )
| A. | 两个关于某直线对称的图形一定全等 | |
| B. | 轴对称的图形对应点的连线的垂直平分线是它们的对称轴 | |
| C. | 对称图形的对称点一定在对称轴的两侧 | |
| D. | 平面上两个全等的图形不一定关于某直线对称 |
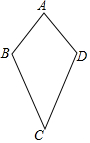 如图所示,已知AB=AD,CB=CD,则在以下各结论中,正确的结论为( )
如图所示,已知AB=AD,CB=CD,则在以下各结论中,正确的结论为( )



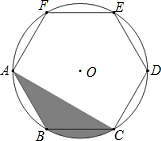 如图,⊙O的半径为4cm,正六边形ABCDEF内接于⊙O,则图中阴影部分面积为$\frac{8π}{3}$cm2.(结果保留π)
如图,⊙O的半径为4cm,正六边形ABCDEF内接于⊙O,则图中阴影部分面积为$\frac{8π}{3}$cm2.(结果保留π)