题目内容
9.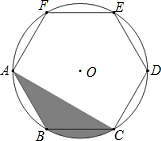 如图,⊙O的半径为4cm,正六边形ABCDEF内接于⊙O,则图中阴影部分面积为$\frac{8π}{3}$cm2.(结果保留π)
如图,⊙O的半径为4cm,正六边形ABCDEF内接于⊙O,则图中阴影部分面积为$\frac{8π}{3}$cm2.(结果保留π)
分析 根据图形分析可得求图中阴影部分面积实为求扇形部分面积,将原图阴影部分面积转化为扇形面积求解即可.
解答 解:如图所示:连接BO,CO,
∵正六边形ABCDEF内接于⊙O,
∴AB=BC=CO=4,∠ABC=120°,△OBC是等边三角形,
∴CO∥AB,
在△COW和△ABW中
$\left\{\begin{array}{l}{∠BWA=∠OWC}\\{∠BAW=∠OCW}\\{AB=CO}\end{array}\right.$,
∴△COW≌△ABW(AAS),
∴图中阴影部分面积为:S扇形OBC=$\frac{60π×{4}^{2}}{360}$=$\frac{8π}{3}$.
故答案为:$\frac{8π}{3}$.
点评 此题主要考查了正多边形和圆以及扇形面积求法,得出阴影部分面积=S扇形OBC是解题关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
19.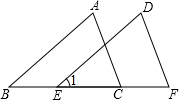 如图,已知∠B=∠1,BE=CF,要使△ABC≌△DEF,下面所添的条件正确的是( )
如图,已知∠B=∠1,BE=CF,要使△ABC≌△DEF,下面所添的条件正确的是( )
 如图,已知∠B=∠1,BE=CF,要使△ABC≌△DEF,下面所添的条件正确的是( )
如图,已知∠B=∠1,BE=CF,要使△ABC≌△DEF,下面所添的条件正确的是( )| A. | AC=DF | B. | BC=EF | C. | AC=EF | D. | AB=DE |
1.下列各式由左边到右边的变形中,是因式分解的是( )
| A. | a2-3a+2=a(a-3) | B. | a2x-a=a(ax-1) | C. | x2+3x+9=(x+3)2 | D. | (x+1)(x-1)=x2-1 |
18.今天教室温度是8℃,室外温度是零下6℃,则室内外温差( )
| A. | 2℃ | B. | 12℃ | C. | 14℃ | D. | 16℃ |

 如图,在△ABC中,AB=AC,∠A=36°,两条角平分线BD、CE相交于点O,则图中全等等腰三角形有3对.
如图,在△ABC中,AB=AC,∠A=36°,两条角平分线BD、CE相交于点O,则图中全等等腰三角形有3对.