题目内容
10.如图是编号分别为1,2,3,…,n的几何图形,这些几何图形都是由若干个互不重叠的三角形组成,例如,编号为1的图形中有1个三角形,编号为2的图形中有4个互不重叠的三角形,编号为3的图形中有7个互不重叠的三角形…,观察图形,解答下列问题: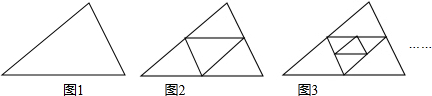
(1)写出编号为n的图形中互不重叠的三角形的个数(用n的代数式表示);
(2)如果编号为m的图形中有298个互不重叠的三角形,求m;
(3)编号为1的题形中的三角形的个数记为S1.编号为2的题形中互不重叠的三角形的个数记为S2,…,编号为n的题形中互不重叠的三角形的个数记为Sn,求:S2-S3+S4-S5…-S99+S100的值.
分析 (1)从前三个图形的变化情况找出规律解答即可;
(2)根据代数式的值求出m即可;
(3)把具体数据代入、根据规律进行计算即可.
解答 解:(1)编号为1的图形中有1个三角形,即3×1-2个;
编号为2的图形中有4个互不重叠的三角形,即3×2-2个;
编号为3的图形中有7个互不重叠的三角形,即3×3-2个;
∴编号为n的图形中互不重叠的三角形的个数是3n-2;
(2)由题意得,3m-2=298,
解得,m=100;
(3)S2-S3+S4-S5…-S99+S100
=4-7+10-13…-295+298
=-3×49+298
=151.
点评 本题考查的是规律性:图形的变化类知识,根据图形的特点和变化情况寻找出正确的变化规律是解题的关键,探寻规律要认真观察、仔细思考,善用联想来解决这类问题..

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
5.下列语句中,正确的是( )
| A. | -$\frac{1}{3}$x=5的解是x=-$\frac{3}{5}$ | B. | 7x=-4的解是x=-$\frac{7}{4}$ | ||
| C. | -x=0的解是x=-1 | D. | $\frac{x}{-10}=0$的解是x=0 |
19.下列说法正确的是( )
| A. | 零表示什么也没有 | |
| B. | 1没有符号 | |
| C. | 零既然不是正数,那是负数 | |
| D. | 一场比赛赢3个球得+3分,-2分表示输了2个球 |
20.根据下列表格对应值:
判断关于x的方程ax2+bx+c=0(a≠0)的一个解x的范围是( )
| x | -1 | 0 | 1 | 1.1 | 1.2 | 1.3 |
| ax2+bx+c | -26 | -15 | -2 | -0.59 | 0.84 | 2.29 |
| A. | x<-1 | B. | -1<x<1 | C. | 1.1<x<1.2 | D. | 1.2<x<1.3 |
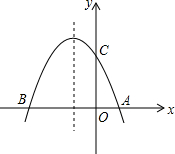 如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于C点,且A(1,0),C(0,3),抛物线的对称轴为x=-1.
如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于C点,且A(1,0),C(0,3),抛物线的对称轴为x=-1. 如图所示,△ABC沿AB向下翻折得到△ABD,若∠ABC=30°,∠ADB=100°,则∠BAC的度数是50°.
如图所示,△ABC沿AB向下翻折得到△ABD,若∠ABC=30°,∠ADB=100°,则∠BAC的度数是50°.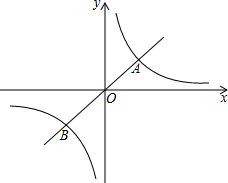 若反比例函数y=$\frac{6}{x}$与正比例函数y=mx的图象相交于点A(a,2)与点B.
若反比例函数y=$\frac{6}{x}$与正比例函数y=mx的图象相交于点A(a,2)与点B.