题目内容
5.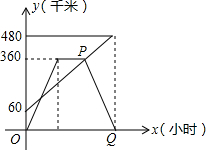 甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图:
甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图:请结合图象信息解答下列问题:
(1)点(0,60)的实际意义是甲车出发时,乙车距离出发地60km,甲车的速度是120千米/时;
(2)①图中点P的坐标是(4,360),点Q的坐标是(7,0);
②求线段PQ的函数关系式;
(3)当两车都朝A地行驶时,问乙车出发多长时间两车相距120干米?
分析 (1)点(0,60)的实际意义是,甲车出发时,乙车距离出发地60km;首先根据图示,可得乙车的速度是60千米/时,然后根据路程÷速度=时间,用两地之间的距离除以乙车的速度,求出乙车到达A地用的时间是多少;最后根据路程÷时间=速度,用两地之间的距离除以甲车往返AC两地用的时间,求出甲车的速度;
(2)①根据甲车与C地的距离及甲车的速度可得甲车离开C地的时间,即可知P的坐标;根据A、B两地距离及乙车速度可得乙车行驶全程所用时间,即可知Q的坐标;
②待定系数法求解可得;
(3)用乙车行驶路程减甲车行驶路程=120列方程求解即可.
解答 解:(1)点(0,60)的实际意义是:甲车出发时,乙车距离出发地60km,
由图可知,乙车的速度是60千米/时,
则甲车的速度是:
(360×2)÷(480÷60-1-1)
=720÷6
=120(千米/小时);
(2)①点P的横坐标为:360÷120+1=4,纵坐标为:360,
故点P的坐标为(4,360),
点Q的横坐标为:480÷60-1=7,
故点Q的坐标为(7,0);
②设线段PQ的解析式为:y=kx+b,
将点P(4,360),Q(7,0)代入,得:
$\left\{\begin{array}{l}{4k+b=360}\\{7k+b=0}\end{array}\right.$,
解得:k=-120,b=840,
故线段PQ的解析式为:y=-120x+840,(4≤x≤7);
(3)设乙车出发x小时后两车相距120千米,
则60x-[120(x-1)-360]=120,
所以480-60x=120,
所以60x=360,
解得x=6.
答:乙车出发6小时两车相距120千米.
故答案为:(1)甲车出发时,乙车距离出发地60km,120;(2)(4,360),(7,0).
点评 此题主要考查了一次函数的应用问题,解答此题的关键是要明确:分段函数是在不同区间有不同对应方式的函数,要特别注意自变量取值范围的划分,既要科学合理,又要符合实际.此题还考查了行程问题,要熟练掌握速度、时间和路程的关系:速度×时间=路程.

 期末集结号系列答案
期末集结号系列答案 如图,在?ABCD中,点E在DC上,BE与AC相交于点F,若$\frac{DE}{EC}$=$\frac{1}{2}$,则$\frac{BF}{BE}$的值为( )
如图,在?ABCD中,点E在DC上,BE与AC相交于点F,若$\frac{DE}{EC}$=$\frac{1}{2}$,则$\frac{BF}{BE}$的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{3}$ |
| A. | 调查全国中学生心理健康现状 | |
| B. | 调查我市食品合格情况 | |
| C. | 调查你所在的班级同学的身高情况 | |
| D. | 调查桂林电视台某电视节目的收视率 |
| A. | 35 | B. | 40 | C. | 45 | D. | 55 |
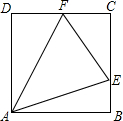 如图,已知正方形ABCD的边长为1,点E,F分别在边BC,CD上,且∠EAF=45°,则△CEF的周长为2.
如图,已知正方形ABCD的边长为1,点E,F分别在边BC,CD上,且∠EAF=45°,则△CEF的周长为2.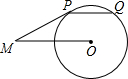 如图,PM切⊙O于点P,弦PQ∥OM,若∠OMP=30°,劣弧PQ的弧长为$\frac{π}{3}$,则线段OM的长为( )
如图,PM切⊙O于点P,弦PQ∥OM,若∠OMP=30°,劣弧PQ的弧长为$\frac{π}{3}$,则线段OM的长为( )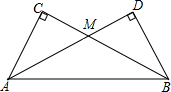 把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点.
把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点.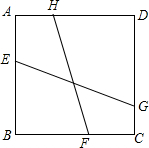 如图,正方形ABCD中,点E、F、G、H分别是在边AB、BC、CD、DA上,且EG与FH的夹角为45°,若正方形ABCD的边长是1.FH=$\frac{\sqrt{5}}{2}$,则EG的长度是$\frac{\sqrt{10}}{3}$.
如图,正方形ABCD中,点E、F、G、H分别是在边AB、BC、CD、DA上,且EG与FH的夹角为45°,若正方形ABCD的边长是1.FH=$\frac{\sqrt{5}}{2}$,则EG的长度是$\frac{\sqrt{10}}{3}$. △ABC中,AD平分∠BAC交BC于D,CH⊥AD于H.
△ABC中,AD平分∠BAC交BC于D,CH⊥AD于H.