题目内容
19. 如图,在平面直角坐标系xOy中,四边形OABC是矩形,点A(4,0),C(0,3).直线y=$\frac{1}{2}x$由原点开始向上平移,所得的直线y=$-\frac{1}{2}x+b$与矩形两边分别交于M、N两点,设△OMN面积为S,那么能表示S与b函数关系的图象大致是( )
如图,在平面直角坐标系xOy中,四边形OABC是矩形,点A(4,0),C(0,3).直线y=$\frac{1}{2}x$由原点开始向上平移,所得的直线y=$-\frac{1}{2}x+b$与矩形两边分别交于M、N两点,设△OMN面积为S,那么能表示S与b函数关系的图象大致是( )| A. |  | B. |  | C. | 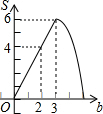 | D. |  |
分析 根据题意可以表示出各段的函数解析式,从而可以得到各段的函数图象,进而得到哪个选项是正确的.
解答 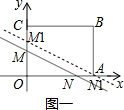 解:当点N从点O移动到点A时,如右图一所示,
解:当点N从点O移动到点A时,如右图一所示,
∵y=$-\frac{1}{2}x+b$与矩形两边分别交于M、N两点,
∴点M的坐标是(0,b),点N的坐标是(2b,0),△OMN面积为S,
∴S与b函数关系式是:$S=\frac{2b•b}{2}={b}^{2}$(0≤b≤2);
当点2≤b≤3时,如图二所示,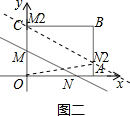
此时点N到OC的距离不变,
∴S=$\frac{b•4}{2}=2b$,
当点b≥3时,如图三所示,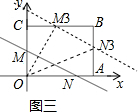
S=S矩形OABC-S△OAN3-S△OCM3-S△M3BN3
=$3×4-\frac{4×(b-2)}{2}-\frac{3×2(b-3)}{2}-\frac{[4-2(b-3)]×[3-(b-2)]}{2}$
=-b2+5b.
故选B.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,求出相应的各段的函数解析式,明确各自对应的函数图象.

练习册系列答案
相关题目
4.已知抛物线y=-(x-m)2的顶点为A,直线l:y=$\sqrt{3}$x-$\sqrt{3}$m,其中m>0
(1)求抛物线的对称轴及点A的坐标(用含m的代数式表示);
(2)证明:点A在直线l上.
(1)求抛物线的对称轴及点A的坐标(用含m的代数式表示);
(2)证明:点A在直线l上.
10. 如图,在?ABCD中,点E在DC上,BE与AC相交于点F,若$\frac{DE}{EC}$=$\frac{1}{2}$,则$\frac{BF}{BE}$的值为( )
如图,在?ABCD中,点E在DC上,BE与AC相交于点F,若$\frac{DE}{EC}$=$\frac{1}{2}$,则$\frac{BF}{BE}$的值为( )
 如图,在?ABCD中,点E在DC上,BE与AC相交于点F,若$\frac{DE}{EC}$=$\frac{1}{2}$,则$\frac{BF}{BE}$的值为( )
如图,在?ABCD中,点E在DC上,BE与AC相交于点F,若$\frac{DE}{EC}$=$\frac{1}{2}$,则$\frac{BF}{BE}$的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{3}$ |
14.下列调查中,适合采用普查的是( )
| A. | 调查全国中学生心理健康现状 | |
| B. | 调查我市食品合格情况 | |
| C. | 调查你所在的班级同学的身高情况 | |
| D. | 调查桂林电视台某电视节目的收视率 |
4.有一个多边形,它的内角和等于它的外角和的2倍,则它是( )
| A. | 三边形 | B. | 四边形 | C. | 五边形 | D. | 六边形 |
9. 如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )
如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )
 如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )
如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )| A. | 40° | B. | 50° | C. | 60° | D. | 30° |
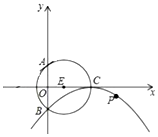 如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=kx+4k+1(k为实数),以点C为顶点的抛物线过点B.
如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=kx+4k+1(k为实数),以点C为顶点的抛物线过点B.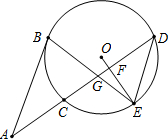 如图,AB切⊙O于点B,AD交⊙O于点C和点D,点E为$\widehat{DC}$的中点,连接OE交CD于点F,连接BE交CD于点G.
如图,AB切⊙O于点B,AD交⊙O于点C和点D,点E为$\widehat{DC}$的中点,连接OE交CD于点F,连接BE交CD于点G.