题目内容
4.已知函数y=(m2+2m)x2+mx+m+1,当m为何值时:(1)这个函数是一次函数;
(2)这个函数是二次函数.
分析 (1)根据二次项系数等于零,一次项系数不等于零,可得答案;
(2)根据二次项系数不等于零,可得答案.
解答 解:(1)由y=(m2+2m)x2+mx+m+1是一次函数,得
$\left\{\begin{array}{l}{{m}^{2}+2m=0}\\{m≠0}\end{array}\right.$,解得m=-2,
当m=-2时,y=(m2+2m)x2+mx+m+1是一次函数;
(2)由y=(m2+2m)x2+mx+m+1是二次函数,得
m2+2m≠0.
解得m≠0,且m≠-2,
当m≠0,且m≠-2时,y=(m2+2m)x2+mx+m+1是二次函数.
点评 本题考查了二次函数的定义,形如y=ax2+bx+c (a≠0)是二次函数,(a=0,b≠0)是一次函数.

练习册系列答案
相关题目
15.在?ABCD中,∠A=36°,则∠C:∠B的值为( )
| A. | 1:3 | B. | 3:1 | C. | 4:1 | D. | 1:4 |
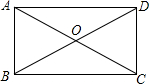 在矩形ABCD中,AC与BD交于点O,∠BOC=120°,AD=6cm,求AC的长.
在矩形ABCD中,AC与BD交于点O,∠BOC=120°,AD=6cm,求AC的长.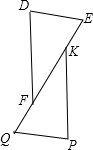 如图,△DEF≌△PQK,DE=5cm,EF=8cm,DF=7cm,QF=3cm.请求出图中其他线段的长度.
如图,△DEF≌△PQK,DE=5cm,EF=8cm,DF=7cm,QF=3cm.请求出图中其他线段的长度.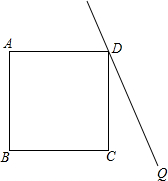 如图,在正方形ABCD外侧作直线DQ,点C关于直线DQ的对称点为P,连接DP、AP,AP交直线DQ于点F,交BD于点E.
如图,在正方形ABCD外侧作直线DQ,点C关于直线DQ的对称点为P,连接DP、AP,AP交直线DQ于点F,交BD于点E.