题目内容
9.已知y=a(x-t-1)2+t2(a,t是常数,a≠0,t≠0)的图象的顶点是A,y=(x-1)2的顶点是B.(1)判断点A是否在y=(x-1)2的图象上,为什么?
(2)若y=a(x-t-1)2+t2(a≠0,t≠0)的图象经过点B,求a的值.
分析 (1)可将A点的坐标代入抛物线y=(x-1)2中,即可判断出A点是否在这条抛物线上.
(2)先根据抛物线y=(x-1)2得出B点的坐标,然后将B点的坐标代入抛物线y=a(x-t-1)2+t2中即可求出a的值.
解答 解:(1)由题意可知:A点的坐标为(t+1,t2),将A点的坐标代入抛物线y=(x-1)2中可得:(t+1-1)2-=t2;
因此A点在抛物线y=(x-1)2的图象上;
(2)由题意可知:B点坐标为(1,0).则有:
0=a(1-t-1)2+t2,即at2+t2=0,因此a=-1.
点评 此题主要考查了二次函数的性质以及二次函数图象上点的特征,根据已知得出A,B点的坐标是解题关键.

练习册系列答案
相关题目
19.二元一次方程组$\left\{\begin{array}{l}{x-y=-3}\\{2x+y=0}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=6}\end{array}\right.$ |
 如图,在△ABC中,CD⊥AB,垂足为D,∠1=∠B,求证:△ABC为直角三角形.
如图,在△ABC中,CD⊥AB,垂足为D,∠1=∠B,求证:△ABC为直角三角形.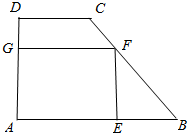 如图,有一块梯形铁板ABCD,AB∥CD,∠A=90°,AB=6cm,CD=2cm,AD=4cm,现在梯形中剪出一内接矩形铁板AEFG,其中E在AB上,F在BC上,G在AD上.若矩形面积为9cm2,则矩形的一边EF长为多少?
如图,有一块梯形铁板ABCD,AB∥CD,∠A=90°,AB=6cm,CD=2cm,AD=4cm,现在梯形中剪出一内接矩形铁板AEFG,其中E在AB上,F在BC上,G在AD上.若矩形面积为9cm2,则矩形的一边EF长为多少?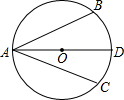 如图,AD为⊙O的直径,AB、AC为弦,且AD平分∠BAC,试判定AB与AC的关系,并证明你的结论.
如图,AD为⊙O的直径,AB、AC为弦,且AD平分∠BAC,试判定AB与AC的关系,并证明你的结论.