题目内容
7．
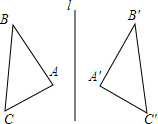如图，△ABC与△A′B′C′关于直线l对称，若∠A=68°，∠C′=38°，则∠B的度数为（ ）| A． | 38° | B． | 74° | C． | 94° | D． | 68° |
分析 根据轴对称的性质得△ABC≌△A′B′C′，则∠C=∠C′=38°，然后根据三角形内角和求∠B的度数．
解答 解：∵△ABC与△A′B′C′关于直线l对称，
∴△ABC≌△A′B′C′
∴∠C=∠C′=38°，
在△ABC中，∠B=180°-∠A-∠C=180°-68°-38°=74°．
故选B．
点评 本题考查了轴对称的性质：如果两个图形关于某直线对称，那么这两个图形全等，对称轴是任何一对对应点所连线段的垂直平分线．
练习册系列答案
相关题目
2．下列各数中，互为相反数的是（ ）
| A． | |-$\frac{3}{2}$|和-$\frac{3}{2}$ | B． | |-$\frac{2}{3}$|和-$\frac{3}{2}$ | C． | |-$\frac{2}{3}$|和$\frac{3}{2}$ | D． | |-$\frac{2}{3}$|和$\frac{2}{3}$ |