题目内容
18.已知α是锐角,且cos(α-15°)=$\frac{\sqrt{3}}{2}$,计算$\sqrt{18}$-6cosα+(3-π)0-tanα-($\frac{1}{2}$)-1的值.分析 利用特殊角的三角函数值,求得α,进一步按照运算顺序,化简二次根式,计算0指数幂,负整数指数幂,特殊角的三角函数值,最后合并即可.
解答 解:∵cos(α-15°)=$\frac{\sqrt{3}}{2}$,
∴α-15°=30°,
∴α=45°,
则$\sqrt{18}$-6cosα+(3-π)0-tanα-($\frac{1}{2}$)-1
=3$\sqrt{2}$-3$\sqrt{2}$+1-1-2
=-2.
点评 此题考查实数的运算,特殊角的三角函数,掌握运算顺序与计算方法是解决问题的关键.

练习册系列答案
相关题目
9. 已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )
已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )
 已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )
已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )| A. | a+b>0 | B. | |a|>|b| | C. | ab<0 | D. | b-a<0 |
13. 如图,在?ABCD中,AB=4,∠A=120°,DE平分∠ADC交BC于点E,则△CDE的周长为( )
如图,在?ABCD中,AB=4,∠A=120°,DE平分∠ADC交BC于点E,则△CDE的周长为( )
 如图,在?ABCD中,AB=4,∠A=120°,DE平分∠ADC交BC于点E,则△CDE的周长为( )
如图,在?ABCD中,AB=4,∠A=120°,DE平分∠ADC交BC于点E,则△CDE的周长为( )| A. | 4$\sqrt{3}$+8 | B. | 4$\sqrt{3}$+4 | C. | 2$\sqrt{3}$+8 | D. | 2$\sqrt{3}$+4 |
10.若(x+3)2=121,则x=( )
| A. | 8 | B. | -14 | ||
| C. | 8或-14 | D. | 以上答案都不正确 |
7.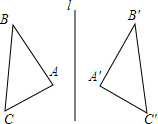 如图,△ABC与△A′B′C′关于直线l对称,若∠A=68°,∠C′=38°,则∠B的度数为( )
如图,△ABC与△A′B′C′关于直线l对称,若∠A=68°,∠C′=38°,则∠B的度数为( )
 如图,△ABC与△A′B′C′关于直线l对称,若∠A=68°,∠C′=38°,则∠B的度数为( )
如图,△ABC与△A′B′C′关于直线l对称,若∠A=68°,∠C′=38°,则∠B的度数为( )| A. | 38° | B. | 74° | C. | 94° | D. | 68° |
 如图,直线DE与直线DF交于点D,△ABC与△A′B′C′关于DE对称.
如图,直线DE与直线DF交于点D,△ABC与△A′B′C′关于DE对称.