题目内容
12.若|2a-1|+|a+2b|=0,则ab=-$\frac{1}{8}$.分析 利用绝对值的性质得出a,b的值,进而代入求出即可.
解答 解:∵|2a-1|+|a+2b|=0,
∴2a-1=0,a+2b=0,
解得:a=$\frac{1}{2}$,b=-$\frac{1}{4}$
则ab=$\frac{1}{2}$×(-$\frac{1}{4}$)=-$\frac{1}{8}$.
故答案为:-$\frac{1}{8}$.
点评 此题主要考查了非负数的性质,得出a,b的值是解题关键.

练习册系列答案
相关题目
20.下列各数:-5,2,-3,1,$\frac{1}{2}$中,正整数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.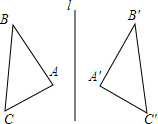 如图,△ABC与△A′B′C′关于直线l对称,若∠A=68°,∠C′=38°,则∠B的度数为( )
如图,△ABC与△A′B′C′关于直线l对称,若∠A=68°,∠C′=38°,则∠B的度数为( )
 如图,△ABC与△A′B′C′关于直线l对称,若∠A=68°,∠C′=38°,则∠B的度数为( )
如图,△ABC与△A′B′C′关于直线l对称,若∠A=68°,∠C′=38°,则∠B的度数为( )| A. | 38° | B. | 74° | C. | 94° | D. | 68° |
17.计算(1-22)×3的结果是( )
| A. | -9 | B. | -11 | C. | 3 | D. | 6 |
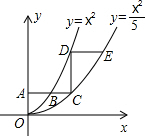 如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=$\frac{{x}^{2}}{5}$(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则$\frac{DE}{AB}$=5-$\sqrt{5}$.
如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=$\frac{{x}^{2}}{5}$(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则$\frac{DE}{AB}$=5-$\sqrt{5}$.