Question

19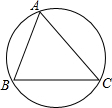．已知△ABC中，角A，B，C所对的边为a，b，c，外接圆的半径为R，证明：$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R．

Answer 1

分析 作辅助线过点O作OD⊥BC于点D，连接OB，OC，利用圆周角与圆心角的关系及三角形的外心可得∠BOD=∠A，利用BD=R×sinA，即$\frac{a}{sinA}$=2R，同理可证明$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R，从而得出结论．

解答 证明：如图，点O为三角形外接圆的圆心，过点O作OD⊥BC于点D，连接OB，OC，

∵点O是△ABC的外心，OD⊥BC，
∴∠BOD=∠COD，
∵∠BOC=2∠A，
∴∠BOD=∠A，
∵OB=2R，
∴BD=R×sinA，即$\frac{1}{2}$a=R×sinA，
∴$\frac{a}{sinA}$=2R，
同理可得$\frac{b}{sinB}$=2R，$\frac{c}{sinC}$=2R，
∴$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R．

点评 本题主要考查了正弦定理，解题的关键是正确作出辅助线利用直角三角形求解．