题目内容
9.已知?ABCD的周长为40,AB=BC-2,则对角线AC的取值范围为( )| A. | 2<AC<20 | B. | 2<AC<40 | C. | 10<AC<20 | D. | 5<AC<21 |
分析 由平行四边形的性质和已知条件得出AB+BC=20,再由BC-AB=2,由三角形的三边关系定理,即可得出结果.
解答 解:如图所示: ∵四边形ABCD是平行四边形,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵?ABCD的周长为40,
∴AB+BC=20,
∵AB=BC-2,
∴BC-AB=2,
在△ABC中,由三角形的三边关系定理得:
BC-AB<AC<BC+AB,
∴对角线AC的取值范围为2<AC<20;
故选:A.
点评 本题考查了平行四边形的性质、三角形的三边关系定理;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
4.如果$\frac{a}{b}$>0,则a与b( )
| A. | 同为正数 | B. | 同为负数 | C. | 同号 | D. | 异号 |
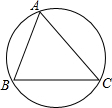 已知△ABC中,角A,B,C所对的边为a,b,c,外接圆的半径为R,证明:$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R.
已知△ABC中,角A,B,C所对的边为a,b,c,外接圆的半径为R,证明:$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R.