Question

8．如图，正方形ABCD中，点E，F分别在边AB，BC上，AF=DE，AF和DE相交于点G．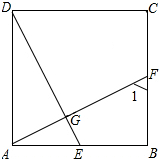
（1）观察图形，直接写出图中所有与∠1相等的角．
（2）选择图中与∠1相等的任意一个角，并加以证明．

Answer 1

分析 （1）由正方形的性质得出AD∥BC，AB∥CD，∠DAE=∠ABF=90°，AD=AB，由平行线的性质得出∠DAG=∠1，∠AED=∠CDE，由HL证明Rt△ADE≌Rt△BAF，得出∠AED=∠1，即可得出∠DAG=∠AED=∠CDE=∠1；
（2）由平行线的性质即可得出∠DAG=∠1．

解答 解：如图所示：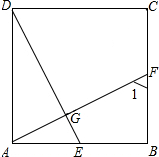
（1）∠DAG=∠AED=∠CDE=∠1；理由如下：
∵四边形ABCD是正方形，
∴AD∥BC，AB∥CD，∠DAE=∠ABF=90°，AD=AB，
∴∠DAG=∠1，∠AED=∠CDE，
在Rt△ADE和Rt△BAF中，$\left\{\begin{array}{l}{DE=AF}\\{AD=AB}\end{array}\right.$，
∴Rt△ADE≌Rt△BAF（HL），
∴∠AED=∠1，
∴∠DAG=∠AED=∠CDE=∠1；
（2）选择∠DAG=∠1；理由如下：
∵四边形ABCD是正方形，
∴AD∥BC，
∴∠DAG=∠1．

点评 本题考查了正方形的性质、平行线的性质、全等三角形的判定与性质；熟练掌握正方形的性质，证明三角形全等是解决问题的突破口．