题目内容
16.已知点A(x1,y1),B(x2,y2)在二次函数y=x2+mx+n的图象上,当x1=1,x2=3时,y1=y2.(1)①求m的值;②若抛物线与x轴只有一个公共点,求n的值;
(2)若P(a,b1),Q(3,b2)是函数图象上的两点,且b1>b2,求实数a的取值范围.
分析 (1)①利用当x1=1,x2=3时函数值相等得到1+m+n=9+3m+n,然后解关于m的方程即可得到m的值;
②根据△=b2-4ac=0时,抛物线与x轴有1个交点得到16-4n=0,然后解关于n的方程即可;
(2)讨论:当P(a,b1),Q(3,b2)在对称轴的右侧,利用二次函数的性质易得a>3时,b1>b2;当P(a,b1),Q(3,b2)在对称轴的两侧,通过比较两点到对称轴的距离的大小可判断a<1时,b1>b2.
解答 解:(1)①∵x1=1,x2=3时,y1=y2,
∴1+m+n=9+3m+n,
∴m=-4;
②∵抛物线与x轴只有一个公共点,
∴△=m2-4n=0,即16-4n=0,
∴n=4;
(2)∵抛物线的对称轴为直线x=1,
∴当P(a,b1),Q(3,b2)在对称轴的右侧,则a>3时,b1>b2;
当P(a,b1),Q(3,b2)在对称轴的两侧,而当x1=1,x2=3时,y1=y2,则a<1时,b1>b2.
∴实数a的取值范围为a<1或a>3.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.也考查了分类讨论思想的运用.

练习册系列答案
相关题目
1.我市2016年某一周每天的最高气温(单位:℃)统计如下:10,16,12,11,14,12,13,则这组数据的众数是( )
| A. | 11 | B. | 12 | C. | 14 | D. | 16 |
5.古希腊数学家把数1,3,6,10,15,21,…叫做三角数,它有一定的规律性.若把第一个三角数记为a1,第二个三角数记为a2…,第n个三角数记为an,则an+an+1=( )
| A. | n2+n | B. | n2+n+1 | C. | n2+2n | D. | n2+2n+1 |
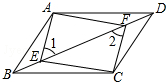 如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,BE=DF.
如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,BE=DF.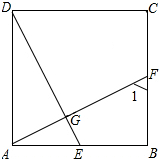
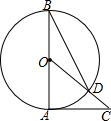 如图,AB是⊙O的直径,AC是⊙O的切线,连接OC与⊙O相交于点D,连接BD,∠C=40°,若点P为优弧$\widehat{ABD}$上的动点,连接PA、PD,则∠APD的大小是25度.
如图,AB是⊙O的直径,AC是⊙O的切线,连接OC与⊙O相交于点D,连接BD,∠C=40°,若点P为优弧$\widehat{ABD}$上的动点,连接PA、PD,则∠APD的大小是25度.