题目内容
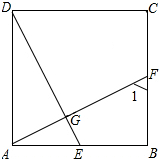
13. 如图,△ABC中,AD是BC边上的高,∠B=2∠C,AD=2,BD=1,则CD的长为1+$\sqrt{5}$.
如图,△ABC中,AD是BC边上的高,∠B=2∠C,AD=2,BD=1,则CD的长为1+$\sqrt{5}$.
分析 在DC上截DM=DB,则AB=AM,∠B=∠AMB=2∠C=2∠CAM,因此AM=CM,从而CD=DM+MC=AB+BD,再利用勾股定理求出AB的长即可.
解答 解:在DC上截DM=DB,
∵AD⊥BC,DM=BD,
∴AD是BM的垂直平分线,
∴AB=AM(线段垂直平分线上的点到线段两端距离相等),
∴∠B=∠AMB(等边对等角),
∵∠B=2∠C,∠AMB=∠C+∠MAC,
∴∠MAC=∠C,
∴AM=CM,
∴CM=AB,
∴CD=DM+MC=BD+AB,
∵在△ABD中,AD=2,BD=1,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴CD=1+$\sqrt{5}$.
故答案为1+$\sqrt{5}$.
点评 本题主要考查了勾股定理、线段垂直平分线的性质等知识,解答本题的关键是添加辅助线证明出CD=DM+MC=BD+AB,此题有一定的难度.

练习册系列答案
相关题目
1.我市2016年某一周每天的最高气温(单位:℃)统计如下:10,16,12,11,14,12,13,则这组数据的众数是( )
| A. | 11 | B. | 12 | C. | 14 | D. | 16 |
5.古希腊数学家把数1,3,6,10,15,21,…叫做三角数,它有一定的规律性.若把第一个三角数记为a1,第二个三角数记为a2…,第n个三角数记为an,则an+an+1=( )
| A. | n2+n | B. | n2+n+1 | C. | n2+2n | D. | n2+2n+1 |
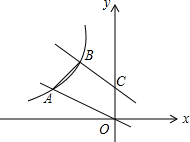 直线y=-x+1交y轴于C点,直线y=-$\frac{1}{2}$x,两条直线分别交双曲线y=$\frac{k}{x}$(x<0)于B、A两点,若$\frac{OA}{BC}$=$\frac{\sqrt{10}}{2}$.
直线y=-x+1交y轴于C点,直线y=-$\frac{1}{2}$x,两条直线分别交双曲线y=$\frac{k}{x}$(x<0)于B、A两点,若$\frac{OA}{BC}$=$\frac{\sqrt{10}}{2}$.