题目内容
11. 如图,点D是等边△ABC内一点,DA=8,BD=10,CD=6,则∠ADC的度数是150°.
如图,点D是等边△ABC内一点,DA=8,BD=10,CD=6,则∠ADC的度数是150°.
分析 将△DBC绕点C顺时针旋转60°得△PAC,根据旋转的性质可证△DCP为等边三角形,由勾股定理的逆定理可证△ADP是直角三角形,从而可求∠ADC的度数.
解答 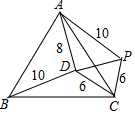 解:将△DBC绕点C顺时针旋转60°得△PAC,
解:将△DBC绕点C顺时针旋转60°得△PAC,
则PC=CD,∠DCP=60°,
∴△CBP为等边三角形,∠PDC=∠PCD=60°,
∵AD=8,BD=10,CD=6,
∴AP=10,PD=CD=6,
∵AD2+DP2=(6)2+(8)2=1002=PA2,
∴△ADP是直角三角形,∠ADP=90°,
∴∠ADC=∠ADP+∠PDC=150°.
故答案为:150°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的判定与性质和等腰直角直角三角形的判定与性质.

练习册系列答案
相关题目
19. 如图,菱形ABCD的周长为8,高AE长为$\sqrt{3}$,则AC:BD=( )
如图,菱形ABCD的周长为8,高AE长为$\sqrt{3}$,则AC:BD=( )
 如图,菱形ABCD的周长为8,高AE长为$\sqrt{3}$,则AC:BD=( )
如图,菱形ABCD的周长为8,高AE长为$\sqrt{3}$,则AC:BD=( )| A. | 1:2 | B. | 1:3 | C. | 1:$\sqrt{2}$ | D. | 1:$\sqrt{3}$ |
16.已知a=$\frac{4}{9}$m-1,b=m2-$\frac{5}{9}$m(m为任意实数),则a与b的大小关系为( )
| A. | a>b | B. | a<b | C. | a=b | D. | 不能确定 |
3.在学校开展的“争做最优秀中学生”的一次演讲比赛中,编号分别为1,2,3,4,5的五位同学最后成绩如下表所示:
那么这五位同学演讲成绩的众数与中位数依次是( )
| 参赛者编号 | 1 | 2 | 3 | 4 | 5 |
| 成绩(分) | 96 | 88 | 86 | 93 | 86 |
| A. | 96,88 | B. | 92,88 | C. | 88,86 | D. | 86,88 |
20.不等式组$\left\{\begin{array}{l}{-2x+3≤5}\\{3(x-1)<x+7}\end{array}\right.$的解集为( )
| A. | x≤-1 | B. | -1≤x<5 | C. | 1≤x<5 | D. | -1≤x<2 |
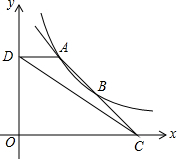 如图,直线y=mx+n与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A、B两点,交x轴于点C($\frac{9}{2}$,0),过点A作AD⊥y轴于点D(0,$\frac{8}{3}$),连接CD,S△ADC=2.
如图,直线y=mx+n与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A、B两点,交x轴于点C($\frac{9}{2}$,0),过点A作AD⊥y轴于点D(0,$\frac{8}{3}$),连接CD,S△ADC=2. 如图,将平行四边形ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠D=114度.
如图,将平行四边形ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠D=114度.