题目内容
9. 已知二次函数y=ax2+b的图象与直线y=x+2相交于点A(1,m)和点B(n,0).
已知二次函数y=ax2+b的图象与直线y=x+2相交于点A(1,m)和点B(n,0).(1)试确定二次函数的解析式;
(2)在给出的平面直角坐标系中画出这个函数图象的草图,并结合图象直接写出ax2+b>x+2时x的取值范围.
分析 (1)先求出AB两点的坐标,再代入二次函数y=ax2+b求出ab的值即可得出其解析式;
(2)在同一坐标系内画出一次函数及二次函数的图象,利用函数图象可直接得出结论.
解答  解:(1)∵直线y=x+2经过点A(1,m)和点B(n,0),
解:(1)∵直线y=x+2经过点A(1,m)和点B(n,0),
∴m=1+2=3,n+2=0,即n=-2,
∴A(1,3),B(-2,0),
∵二次函数y=ax2+b的图象经过A(1,3),B(-2,0),
∴$\left\{\begin{array}{l}a+b=3\\ 4a+b=0\end{array}\right.$,解得$\left\{\begin{array}{l}a=-1\\ b=4\end{array}\right.$,
∴二次函数的解析式为y=-x2+4;
(2)如图,由函数图象可知,当-2<x<1时,ax2+b>x+2.
点评 本题考查的是二次函数与不等式,能根据题意画出图形,利用数形结合求出不等式的解集是解答此题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
4.若抛物线y=(x-a)2+(a-1)的顶点在第一象限,则a的取值范围为( )
| A. | a>1 | B. | a>0 | C. | a>-1 | D. | -1<a<0 |
1.不解方程,判断一元二次方程3x2+4x-3=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
18.下列各数中,不属于正数的是( )
| A. | -0.2 | B. | 5.5 | C. | $\frac{1}{5}$ | D. | 20 |
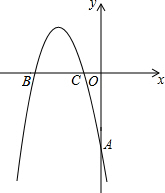 如图,在平面直角坐标系中,抛物线y=-$\frac{2}{3}$x2+bx+c,经过A(0,-4)、它的对称轴为 x=-$\frac{7}{2}$,它与x轴相交于B、C.
如图,在平面直角坐标系中,抛物线y=-$\frac{2}{3}$x2+bx+c,经过A(0,-4)、它的对称轴为 x=-$\frac{7}{2}$,它与x轴相交于B、C.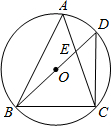 已知如图,△ABC内接于⊙O,∠A=50°,∠ABC=60°,BD是⊙O的直径,BD=10,BD交AC于点E,连接DC.
已知如图,△ABC内接于⊙O,∠A=50°,∠ABC=60°,BD是⊙O的直径,BD=10,BD交AC于点E,连接DC.