��Ŀ����
19��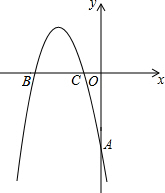 ��ͼ����ƽ��ֱ������ϵ�У�������y=-$\frac{2}{3}$x2+bx+c������A��0��-4�������ĶԳ���Ϊ x=-$\frac{7}{2}$������x���ཻ��B��C��
��ͼ����ƽ��ֱ������ϵ�У�������y=-$\frac{2}{3}$x2+bx+c������A��0��-4�������ĶԳ���Ϊ x=-$\frac{7}{2}$������x���ཻ��B��C����1����b��c��ֵ��
��2��������������һ��D��ʹ�ö�����һ��E���ı���BDCE����BCΪ�Խ��ߵ����Σ�
��3�������������Ƿ����һ��P��ʹ���ı���BPOH����OBΪ�Խ��ߵ����Σ������ڣ������P�����꣬���ж���������Ƿ�Ϊ�����Σ��������ڣ���˵�����ɣ�
���� ��1������A�����꣬�ɵ�c��ֵ�����ݶԳ��ṫʽ���ɵ�b��ֵ��
��2���������εĶԳ��ᴹֱ�һ���ƽ�֣��ɵ�D�������ߵĶ��㣻
��3���������εĶԽ��ߴ�ֱ�һ���ƽ�֣��ɵ�P��ֱ��x=-3��������y=-$\frac{2}{3}$x2-$\frac{14}{3}$x-4�Ľ��㣬�����Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵô𰸣����������εĶԽ�������һ���ƽ�֡���ֱ���ɵô𰸣�
��� �⣺��1����������y=-$\frac{2}{3}$x2+bx+c������A��0��-4����
��c=-4��
�Գ���x=-$\frac{b}{2����-\frac{2}{3}��}$=-$\frac{7}{2}$��
���b=-$\frac{14}{3}$��
��2�����ı���BDCE����BCΪ�Խ��ߵ����Σ��������ε����ʣ���D���������ߵĶԳ����ϣ�
�֡�y=-$\frac{2}{3}$x2-$\frac{14}{3}$x-4=-$\frac{2}{3}$��x+$\frac{7}{2}$��2+$\frac{25}{6}$
�������ߵĶ��㣨-$\frac{7}{2}$��$\frac{25}{6}$����Ϊ����ĵ�D��
��3����y=0ʱ��-$\frac{2}{3}$x2-$\frac{14}{3}$x-4=0�����x=-6��x=-1����B��-6��0����
���ı���BPOH����OBΪ�Խ��ߵ����Σ���B������Ϊ��-6��0����
��P����ֱ��x=-3��������y=-$\frac{2}{3}$x2-$\frac{14}{3}$x-4�Ľ��㣬
�൱x=-3ʱ��y=-$\frac{2}{3}$����-3��2-$\frac{14}{3}$����-3��-4=4��
�����������ϴ���һ��P��-3��4����ʹ���ı���BPOHΪ���Σ�
�ı���BPOH���ܳ�Ϊ�����Σ�
������ı���BPOHΪ�����Σ���P������ֻ���ǣ�-3��3��������һ�㲻���������ϣ�
�ı���BPOH���ܳ�Ϊ�����Σ�
���� ���⿼���˶��κ����ۺ��⣬�����˶Գ��ṫʽ�����ε����ʣ����εĶԽ��ߴ�ֱ�һ���ƽ�֣������ε����ʣ������εĶԽ�������һ���ƽ�֡���ֱ��

| A�� | ��4x=2x-1����4x-2x=1 | B�� | ��-2x=4����x=2 | ||
| C�� | ��5x-3=4����5x=4-3 | D�� | ��-3x-2=2x+3����-3x-2x=3+2 |
 ��ͼ��ʾ��DE�ǡ�ABC����λ�ߣ���F��DE�ϣ��ҡ�AFB=90�㣬��AB=5��BC=8����EF�ij�Ϊ��������
��ͼ��ʾ��DE�ǡ�ABC����λ�ߣ���F��DE�ϣ��ҡ�AFB=90�㣬��AB=5��BC=8����EF�ij�Ϊ��������| A�� | $\frac{3}{2}$ | B�� | 4 | C�� | $\frac{5}{2}$ | D�� | 1 |
 ��ͼ��E���߶�AB�е㣬F���߶�AE�е㣬��֪ͼ�������߶εij���֮��Ϊ52�����߶�AE�ij���
��ͼ��E���߶�AB�е㣬F���߶�AE�е㣬��֪ͼ�������߶εij���֮��Ϊ52�����߶�AE�ij���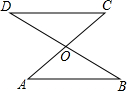 ��ͼ��AC��BD���ڵ�O��ͼ�й���8���߶Σ����Ƿֱ���CD��OC��OA��OD��OB��BD��AC��AB��
��ͼ��AC��BD���ڵ�O��ͼ�й���8���߶Σ����Ƿֱ���CD��OC��OA��OD��OB��BD��AC��AB��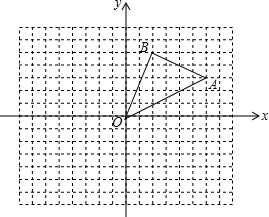 ��ͼ���ڱ߳�Ϊ1����������ɵ������У���AOB�Ķ�����ڸ���ϣ���A��B������ֱ�Ϊ��6��3������2��5��
��ͼ���ڱ߳�Ϊ1����������ɵ������У���AOB�Ķ�����ڸ���ϣ���A��B������ֱ�Ϊ��6��3������2��5��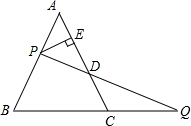 ��ͼ��P�ǵȱߡ�ABC��AB����һ�㣬��P��PE��AC��E����BC���ӳ����Ͻ�ȡCQ=AP������PQ��AC�ڵ�D��
��ͼ��P�ǵȱߡ�ABC��AB����һ�㣬��P��PE��AC��E����BC���ӳ����Ͻ�ȡCQ=AP������PQ��AC�ڵ�D�� ��֪���κ���y=ax2+b��ͼ����ֱ��y=x+2�ཻ�ڵ�A��1��m���͵�B��n��0����
��֪���κ���y=ax2+b��ͼ����ֱ��y=x+2�ཻ�ڵ�A��1��m���͵�B��n��0����