题目内容
20.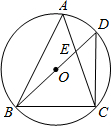 已知如图,△ABC内接于⊙O,∠A=50°,∠ABC=60°,BD是⊙O的直径,BD=10,BD交AC于点E,连接DC.
已知如图,△ABC内接于⊙O,∠A=50°,∠ABC=60°,BD是⊙O的直径,BD=10,BD交AC于点E,连接DC.(1)求∠AEB的度数;
(2)求弦AC的长度.
分析 (1)因为∠A=50°,∠ABC=60°,所以利用三角形的内角和可得∠ACB=70°,利用同弧所对的圆周角相等可得∠A=∠D=50°,又因为∠BCD是直径所对的圆周角,所以等于90°,因此可得∠ECD=20°,利用内角和与对顶角相等可得∠AEB等于110°;
(2)连接AO.CO,过O作OH⊥AC于H,根据圆周角定理得到∠AOH=60°,根据三角函数的定义得到AH=AO•$\frac{\sqrt{3}}{2}$=$\frac{5\sqrt{3}}{2}$,根据等腰三角形的性质即可得到结论.AC=2AH=5$\sqrt{3}$.
解答  解:(1)如图1,连接AE,
解:(1)如图1,连接AE,
∵∠A=50°,∠ABC=60°,
∴∠ACB=70°,
∵BD是圆O的直径,
∴∠BCD=90°,
∴∠ACD=20°,
∴∠ABD=∠ACD=20°,
∴∠AEB=180°-(∠BAE+∠ABE)=180°-(50°+20°)=110°;
(2)如图2, 连接AO.CO,过O作OH⊥AC于H,
连接AO.CO,过O作OH⊥AC于H,
∵∠ABC=60°,
∴∠AOH=60°,
∵BD=10,
∴AO=5,
∴AH=AO•$\frac{\sqrt{3}}{2}$=$\frac{5\sqrt{3}}{2}$,
∵OA=OC,
∴AC=2AH=5$\sqrt{3}$.
点评 本题重点考查了直径所对的圆周角是直角,同弧所对的圆周角相等,三角形的内角和等知识点,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
8. 如图所示,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
如图所示,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
 如图所示,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
如图所示,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )| A. | $\frac{3}{2}$ | B. | 4 | C. | $\frac{5}{2}$ | D. | 1 |
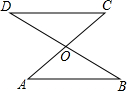 如图.AC,BD交于点O.图中共有8条线段,它们分别是CD,OC,OA,OD,OB,BD,AC,AB.
如图.AC,BD交于点O.图中共有8条线段,它们分别是CD,OC,OA,OD,OB,BD,AC,AB.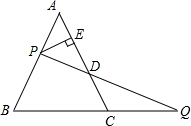 如图,P是等边△ABC的AB边上一点,过P作PE⊥AC于E,在BC的延长线上截取CQ=AP,连接PQ交AC于点D.
如图,P是等边△ABC的AB边上一点,过P作PE⊥AC于E,在BC的延长线上截取CQ=AP,连接PQ交AC于点D. 已知二次函数y=ax2+b的图象与直线y=x+2相交于点A(1,m)和点B(n,0).
已知二次函数y=ax2+b的图象与直线y=x+2相交于点A(1,m)和点B(n,0).