题目内容
7.计算:(1)(-$\frac{7}{3}$)÷(-1$\frac{1}{6}$)-$\frac{3}{4}$×(-2$\frac{2}{3}$)
(2)-62-(3-7)2-2×(-1)3-|-2|
(3)180°-(78°35′+26°40′)
(4)3x2-[7x(4x-3)-2x2].
分析 (1)先算乘除,再算加减即可;
(2)先算乘方,再算乘法,最后算加减即可;
(3)先算括号里面的,再算减法即可;
(4)先去括号,再合并同类项即可.
解答 解:(1)原式=-$\frac{7}{3}$×(-$\frac{6}{7}$)-$\frac{3}{4}$×(-$\frac{8}{3}$)
=2+2
=4;
(2)原式=-36-16+2-2
=-52;
(3)原式=180°-(78°35′+26°40′)
=180°-105°15′
=74°45′;
(4)原式=3x2-[26x2-21x]
=3x2-26x2+21x
=-23x2+21x.
点评 本题考查的是有理数的混合运算,熟知有理数混合运算的法则是解答此题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
9.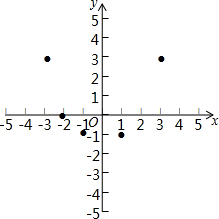 有这样一个问题:探究函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质.
有这样一个问题:探究函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质.
小峰根据学习函数的经验,对函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质进行了探究.
下面是小峰的探究过程,请补充完整:
(1)函数y=x2-2$\sqrt{{x}^{2}}$的自变量的取值范围是任意实数;
(2)下表是y与x的几组对应值.
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第四象限内的最低点是(1,-1),结合函数的图象,写出该函数的其它性质(一条即可):对称轴是y轴.
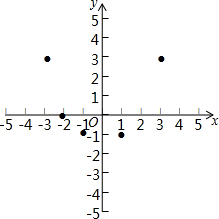 有这样一个问题:探究函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质.
有这样一个问题:探究函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质.小峰根据学习函数的经验,对函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质进行了探究.
下面是小峰的探究过程,请补充完整:
(1)函数y=x2-2$\sqrt{{x}^{2}}$的自变量的取值范围是任意实数;
(2)下表是y与x的几组对应值.
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | n | 3 | 0 | -1 | 0 | -1 | 0 | 3 | m | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第四象限内的最低点是(1,-1),结合函数的图象,写出该函数的其它性质(一条即可):对称轴是y轴.




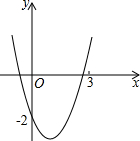 如图,已知抛物线y=x2+bx+c经过点(0,-2),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.你所确定的b的值为-$\frac{7}{3}$<b<1.
如图,已知抛物线y=x2+bx+c经过点(0,-2),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.你所确定的b的值为-$\frac{7}{3}$<b<1.