题目内容
18.下图中阴影部分的面积与函数y=$\frac{1}{2}$(x-1)2+$\frac{3}{2}$的最小值相同的是( )| A. |  | B. |  | C. |  | D. |  |
分析 分别利用一次函数、反比例函数以及二次函数的性质得出各选项中阴影部分面积,进而得出答案.
解答 解:函数y=$\frac{1}{2}$(x-1)2+$\frac{3}{2}$的最小值为:$\frac{3}{2}$,
A、阴影部分面积为:1,故此选项错误;
B、由图可得:阴影部分面积为:1×3×$\frac{1}{2}$=$\frac{3}{2}$,故此选项正确;
C、由图可得:阴影部分面积为:2×1×$\frac{1}{2}$=1,故此选项错误;
D、由图可得:阴影部分面积为:2×1×$\frac{1}{2}$=1,故此选项错误.
故选:B.
点评 此题主要考查了二次函数的性质、一次函数图象上点的特征以及反比例函数系数k的几何意义,熟练应用相关性质是解题关键.

练习册系列答案
相关题目
8.要使分式$\frac{x+3}{(x+3)(x-4)}$有意义,则x应满足( )
| A. | x≠-3 | B. | x≠4 | C. | x≠±3 | D. | x≠-3且x≠4 |
13.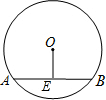 如图,已知⊙O的半径为10cm,弦AB的长为12cm,则弦AB的弦心距OE的长为( )
如图,已知⊙O的半径为10cm,弦AB的长为12cm,则弦AB的弦心距OE的长为( )
 如图,已知⊙O的半径为10cm,弦AB的长为12cm,则弦AB的弦心距OE的长为( )
如图,已知⊙O的半径为10cm,弦AB的长为12cm,则弦AB的弦心距OE的长为( )| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
1.抛物线y=x2+mx+n可以由抛物线y=x2向上平移2个单位,再向左平移3个单位得到,则mn值为( )
| A. | 6 | B. | 12 | C. | 54 | D. | 66 |
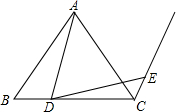 如图,等腰△ABC,AB=AC,D是BC边上一点,射线CE∥AB,且AD=DE,
如图,等腰△ABC,AB=AC,D是BC边上一点,射线CE∥AB,且AD=DE,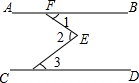 如图,AB∥CD,∠2=70°,则∠1+∠2+∠3的度数为140°.
如图,AB∥CD,∠2=70°,则∠1+∠2+∠3的度数为140°. 小李画了一个二次函数y=2x2+ax+b的图象如图所示,则关于x的方程2x2+ax+b=0的解是x=-1或x=4.
小李画了一个二次函数y=2x2+ax+b的图象如图所示,则关于x的方程2x2+ax+b=0的解是x=-1或x=4.