题目内容
17.解下列方程(组)(1)3(2x-1)+4=1-(2x-1)
(2)$\frac{4x+3}{6}+\frac{4x+3}{2}+\frac{4x+3}{3}=1$
(3)$\left\{\begin{array}{l}{x-2y=6}\\{2x+3y=7}\end{array}\right.$
(4)$\left\{\begin{array}{l}{4x-2y=14}\\{x+y=5}\end{array}\right.$.
分析 (1)方程去括号,移项合并,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(3)方程组利用加减消元法求出解即可;
(4)方程组利用加减消元法求出解即可.
解答 解:(1)去括号得:6x-3+4=1-2x+1,
移项合并得:8x=1,
解得:x=0.125;
(2)去分母得:4x+3+12x+9+8x+6=6,
移项合并得:24x=-12,
解得:x=-0.5;
(3)$\left\{\begin{array}{l}{x-2y=6①}\\{2x+3y=7②}\end{array}\right.$,
②-①×2得:7y=-5,即y=-$\frac{5}{7}$,
把y=-$\frac{5}{7}$代入①得:x=$\frac{32}{7}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{32}{7}}\\{y=-\frac{5}{7}}\end{array}\right.$;
(4)方程组整理得:$\left\{\begin{array}{l}{2x-y=7①}\\{x+y=5②}\end{array}\right.$,
①+②得:3x=12,即x=4,
把x=4代入②得:y=1,
则方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,以及解一元一次方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
8.要使分式$\frac{x+3}{(x+3)(x-4)}$有意义,则x应满足( )
| A. | x≠-3 | B. | x≠4 | C. | x≠±3 | D. | x≠-3且x≠4 |
12.如果2x=4y+1,27y=3x-1,则x-y等于( )
| A. | 3 | B. | -3 | C. | -1 | D. | 1 |
2.某商店在一次买卖中,同时卖出两种货物,每种货物的售价均为960元.若按成本计算,一种货物盈利20%,另一种亏本20%,则这次交易商店( )
| A. | 赚160元 | B. | 赔80元 | C. | 赔240元 | D. | 赚400元 |
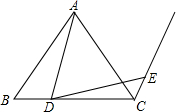 如图,等腰△ABC,AB=AC,D是BC边上一点,射线CE∥AB,且AD=DE,
如图,等腰△ABC,AB=AC,D是BC边上一点,射线CE∥AB,且AD=DE,