题目内容
19.一个多边形的内角和与外角和的差是180°,则这个多边形的对角线为5条.分析 设出这个多边形的边数,利用内角和与外角和的差是180°列出相应等式,即可求得多边形的边数;易得过n边形的一个顶点可画出(n-3)条对角线,那么过n个顶点可以画出n(n-3)条对角线,根据两点确定一条直线,再把所得结果除以2即可求得多边形的对角线的总条数.
解答 解:设多边形的边数为n,
则(n-2)×180-360=180,
解得n=5.
∴对角线的条数=$\frac{5×(5-3)}{2}$=5.
答:对角线的条数是5.
故答案为:5.
点评 本题考查了多边形的内角和与外角和定理,任意多边形的外角和都是360°,与边数无关.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.抛物线y=x2+mx+n可以由抛物线y=x2向上平移2个单位,再向左平移3个单位得到,则mn值为( )
| A. | 6 | B. | 12 | C. | 54 | D. | 66 |
2.下列各式不能用平方差公式计算的是( )
| A. | (a2-b)(a2+b) | B. | (-a+b)(a-b) | C. | (-2a+b)(b-2a) | D. | (-2a+b)(b+2a) |
 小李画了一个二次函数y=2x2+ax+b的图象如图所示,则关于x的方程2x2+ax+b=0的解是x=-1或x=4.
小李画了一个二次函数y=2x2+ax+b的图象如图所示,则关于x的方程2x2+ax+b=0的解是x=-1或x=4.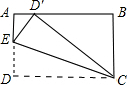 如图,在正方形ABCD,AD=6,AB=10,在AD上取一点E,将△EDC沿EC折叠,使D点恰好落在AB边上的D′点,求DE的长.
如图,在正方形ABCD,AD=6,AB=10,在AD上取一点E,将△EDC沿EC折叠,使D点恰好落在AB边上的D′点,求DE的长.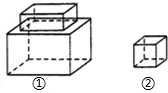 某玩具加工厂要制造如图所示的两种形状的玩具配件,其中,配件①是由大、小两个长方体构成的,大长方体的长、宽、高分别为:$\frac{5}{2}$a、2a、$\frac{3}{2}$a,小长方体的长、宽、高分别为:2a、a、$\frac{a}{2}$;配件②是一个正方体,其边长为a
某玩具加工厂要制造如图所示的两种形状的玩具配件,其中,配件①是由大、小两个长方体构成的,大长方体的长、宽、高分别为:$\frac{5}{2}$a、2a、$\frac{3}{2}$a,小长方体的长、宽、高分别为:2a、a、$\frac{a}{2}$;配件②是一个正方体,其边长为a