题目内容
15.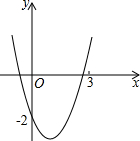 如图,已知抛物线y=x2+bx+c经过点(0,-2),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.你所确定的b的值为-$\frac{7}{3}$<b<1.
如图,已知抛物线y=x2+bx+c经过点(0,-2),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.你所确定的b的值为-$\frac{7}{3}$<b<1.
分析 把(0,-2)代入抛物线的解析式求出c的值;在(1,0)和(3,0)之间取一个点,分别把x=1和x=3时的坐标代入解析式即可得出不等式组,求出答案即可.
解答 解:把(0,-2)代入抛物线的解析式得:c=-2,
∴y=x2+bx-2,
∵使该抛物线与x轴的一个交点在(1,0)和(3,0)之间,
∴把x=1代入y=x2+bx-2得:y=1+b-2<0
把x=3代入y=x2+bx-2得:y=9+3b-2>0,
∴-$\frac{7}{3}$<b<1,
即在-2<b<2范围内的任何一个数都符合.
故答案为:-1(在-$\frac{7}{3}$<b<1范围内的任何一个数).
点评 本题主要考查对抛物线与x轴的交点的理解和掌握,能理解抛物线与x轴的交点的坐标特点是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
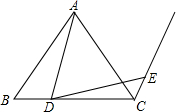 如图,等腰△ABC,AB=AC,D是BC边上一点,射线CE∥AB,且AD=DE,
如图,等腰△ABC,AB=AC,D是BC边上一点,射线CE∥AB,且AD=DE,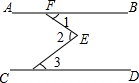 如图,AB∥CD,∠2=70°,则∠1+∠2+∠3的度数为140°.
如图,AB∥CD,∠2=70°,则∠1+∠2+∠3的度数为140°. 小李画了一个二次函数y=2x2+ax+b的图象如图所示,则关于x的方程2x2+ax+b=0的解是x=-1或x=4.
小李画了一个二次函数y=2x2+ax+b的图象如图所示,则关于x的方程2x2+ax+b=0的解是x=-1或x=4.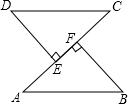 已知:如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,DE=BF.
已知:如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,DE=BF.