题目内容
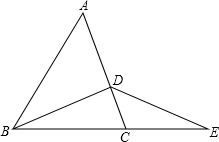 如图:D为AC上一点,E为BC延长线上一点,连接BD,DE.
如图:D为AC上一点,E为BC延长线上一点,连接BD,DE.(1)∠ADB与∠DCB的大小关系是:∠ADB
(2)判断∠ADB与∠CDE的大小关系,并证明你的判断.
考点:三角形的外角性质
专题:
分析:(1)根据三角形外角的定义进行解答;
(2)根据三角形外角定理得到:∠ADB=∠DBC+∠DCB,∠DCB=∠CDE+∠E,易证∠ADB>∠CDE.
(2)根据三角形外角定理得到:∠ADB=∠DBC+∠DCB,∠DCB=∠CDE+∠E,易证∠ADB>∠CDE.
解答:解:(1)∵∠DBC+∠BCD=∠BDA,
∴∠ADB>∠ACB,
故答案为:>;
(2)∠ADB>∠CDE.理由如下:
∵∠ADB=∠DBC+∠DCB,∠DCB=∠CDE+∠E,
∴∠ADB>∠CDE.
∴∠ADB>∠ACB,
故答案为:>;
(2)∠ADB>∠CDE.理由如下:
∵∠ADB=∠DBC+∠DCB,∠DCB=∠CDE+∠E,
∴∠ADB>∠CDE.
点评:本题考查了三角形的外角性质:三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
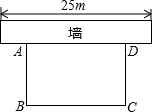 如图所示:某居民小区要在一块要边靠墙(墙长25m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边由总长为40m的栅栏围成.
如图所示:某居民小区要在一块要边靠墙(墙长25m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边由总长为40m的栅栏围成.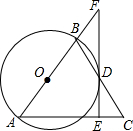 如图在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于E交AB的延长线于点F,
如图在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于E交AB的延长线于点F,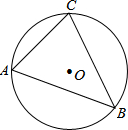 如图,圆O是△ABC的外接圆,圆O的半径为6,∠ABC=45°,求AC的长.
如图,圆O是△ABC的外接圆,圆O的半径为6,∠ABC=45°,求AC的长.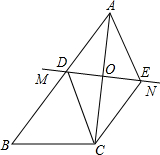 如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于E,连结AE、CD.
如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于E,连结AE、CD. 如图所示,若菱形OABC的顶点O为坐标原点,点C在x轴上,直线y=x经过点A,菱形面积是
如图所示,若菱形OABC的顶点O为坐标原点,点C在x轴上,直线y=x经过点A,菱形面积是