题目内容
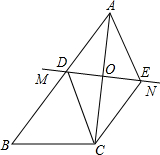 如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于E,连结AE、CD.
如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于E,连结AE、CD.(1)求证:AD=CE;
(2)试判断四边形ADCE的形状,并说明理由.
考点:菱形的判定,全等三角形的判定与性质,线段垂直平分线的性质
专题:
分析:(1)根据中垂线的性质:中垂线上的点线段两个端点的距离相等,得出AE=CE,AD=CD,OA=OC,∠AOD=∠EOC=90°,由CE∥AB,得到∠DAO=∠ECO,利用AAS证明△ADO≌△CEO,即可得出OD=OE;
(2)由一组对边平行且相等知,四边形ADCE是平行四边形,再根据对角线互相垂直的平行四边形是菱形得平行四边形ADCE是菱形.
(2)由一组对边平行且相等知,四边形ADCE是平行四边形,再根据对角线互相垂直的平行四边形是菱形得平行四边形ADCE是菱形.
解答:(1)证明:∵MN是AC的垂直平分线,
∴OA=OC,∠AOD=∠EOC=90°.
∵CE∥AB,
∴∠DAO=∠ECO,
在△ADO与△CEO中,
,
∴△ADO≌△CEO(ASA),
∴OD=OE;
(2)解:四边形ADCE是菱形.理由如下:
由(1)得OA=OC,AD=CE,
∴四边形ADCE是平行四边形,
∵AC⊥DE,
∴平行四边形ADCE是菱形.
∴OA=OC,∠AOD=∠EOC=90°.
∵CE∥AB,
∴∠DAO=∠ECO,
在△ADO与△CEO中,
|
∴△ADO≌△CEO(ASA),
∴OD=OE;
(2)解:四边形ADCE是菱形.理由如下:
由(1)得OA=OC,AD=CE,
∴四边形ADCE是平行四边形,
∵AC⊥DE,
∴平行四边形ADCE是菱形.
点评:本题考查了中垂线的性质,全等三角形的判定和性质,菱形的判定,证明△ADO≌△CEO,得出OD=OE是解题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
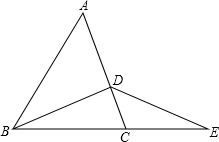 如图:D为AC上一点,E为BC延长线上一点,连接BD,DE.
如图:D为AC上一点,E为BC延长线上一点,连接BD,DE.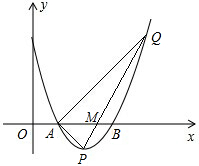 如图,二次函数图象的顶点是P(2,-1),与x轴交于点A和点B(3,0)
如图,二次函数图象的顶点是P(2,-1),与x轴交于点A和点B(3,0)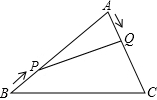 如图,在△ABC中,∠A=60°,AB=18,AC=12,点P从点B出发,以3cm/s的速度向点A运动,点Q从点A同时出发以2cm/s的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动.
如图,在△ABC中,∠A=60°,AB=18,AC=12,点P从点B出发,以3cm/s的速度向点A运动,点Q从点A同时出发以2cm/s的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动.