题目内容
因式分解:
(1)4x2-64
(2)4ab2-4a2b-b3
(3)16(m-n)2-9(m+n)2
(4)x2(x-y)+(y-x)
(1)4x2-64
(2)4ab2-4a2b-b3
(3)16(m-n)2-9(m+n)2
(4)x2(x-y)+(y-x)
考点:提公因式法与公式法的综合运用
专题:计算题
分析:(1)原式提取公因式后,利用平方差公式分解即可;
(2)原式提取公因式,利用完全平方公式分解即可;
(3)原式利用平方差公式分解即可;
(4)原式提取公因式后,利用平方差公式分解即可.
(2)原式提取公因式,利用完全平方公式分解即可;
(3)原式利用平方差公式分解即可;
(4)原式提取公因式后,利用平方差公式分解即可.
解答:解:(1)4x2-64=4(x2-16)=4(x+4)(x-4);
(2)4ab2-4a2b-b3=-b(4a2-4ab+b2)=-b(2a-b)2;
(3)16(m-n)2-9(m+n)2=[4(m-n)+3(m+n)][4(m-n)-3(m+n)]=(7m-n)(m-7n);
(4)x2(x-y)+(y-x)=(x-y)(x+1)(x-1).
(2)4ab2-4a2b-b3=-b(4a2-4ab+b2)=-b(2a-b)2;
(3)16(m-n)2-9(m+n)2=[4(m-n)+3(m+n)][4(m-n)-3(m+n)]=(7m-n)(m-7n);
(4)x2(x-y)+(y-x)=(x-y)(x+1)(x-1).
点评:此题考查了提公因式与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
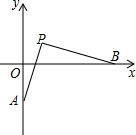 如图,平面直角坐标系中,已知P(1,1),A为y轴的负半轴上一点,B为x轴的正半轴上一点,PA=PB.
如图,平面直角坐标系中,已知P(1,1),A为y轴的负半轴上一点,B为x轴的正半轴上一点,PA=PB.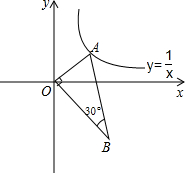 已知,如图,在平面直角坐标系中,AO⊥BO,∠B=30°,点A在反比例函数y=
已知,如图,在平面直角坐标系中,AO⊥BO,∠B=30°,点A在反比例函数y=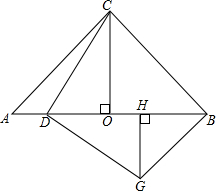 在等腰Rt△ABC中,∠ACB=90°,CO⊥AB,D为AO上一点,过点D作CD的垂线,过B点作BC的垂线,两垂线交于的G,过G作GH⊥AB,求证:CO=DH.
在等腰Rt△ABC中,∠ACB=90°,CO⊥AB,D为AO上一点,过点D作CD的垂线,过B点作BC的垂线,两垂线交于的G,过G作GH⊥AB,求证:CO=DH.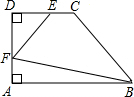 如图所示,在直角梯形ABCD中,∠A=∠D=90°,E、F分别是DC、DA边上,且DE=AF,已知DC=3,AD=4,AB=6,设DE=x,四边形EFBC的面积是S.
如图所示,在直角梯形ABCD中,∠A=∠D=90°,E、F分别是DC、DA边上,且DE=AF,已知DC=3,AD=4,AB=6,设DE=x,四边形EFBC的面积是S.